Paso 17: Un Tweak menor: Ley de Control de la raíz cuadrada
![]()
Mucho de la teoría de control utilizada en este proyecto, particularmente la analogía masa-resorte-amortiguador para el controlador PD, se basa en el hecho de que los motores producen empuje proporcional para ángulo de error, o velocidad angular. Los comandos enviados al motor no son valores de empuje, aunque. Representan una tensión, o más precisamente una fracción de la tensión de la batería, aplicada en los bornes del motor. La tensión y la velocidad del motor están estrechamente relacionados, razón por la cual controladores de motor son a menudo llamados controladores de velocidad. Pero el empuje está más estrechamente relacionada con el
cuadrado de la velocidad de la hélice. (Al igual que
la elevación es proporcional al cuadrado de la velocidad).
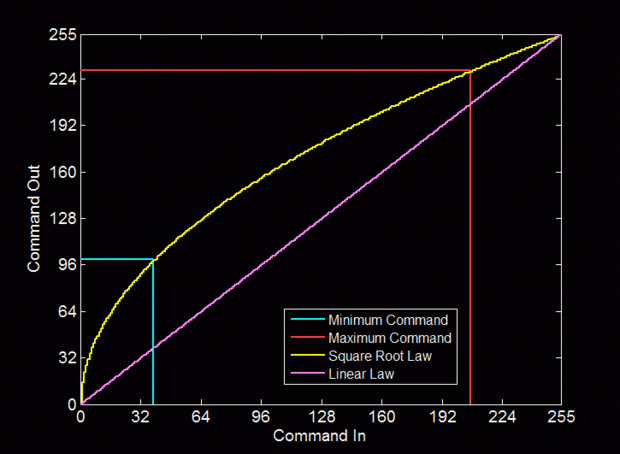
Puesto que el cuadrotor pasa la mayor parte de su tiempo en un pequeño grupo de velocidades alrededor de libración, la diferencia puede importa mucho. Pero jugaba con la idea de "deshacer" la relación cuadrada pasando los comandos de motor a través de una función raíz cuadrada antes de enviarlos a los motores. La función raíz cuadrada debe ser normalizado (véase la imagen), pero se puede hacer con una tabla de búsqueda para el tiempo de CPU disponible.
Encontré que esta modificación mejora la estabilidad, especialmente para sostener manualmente la altitud.