Paso 11: Usando el GPS
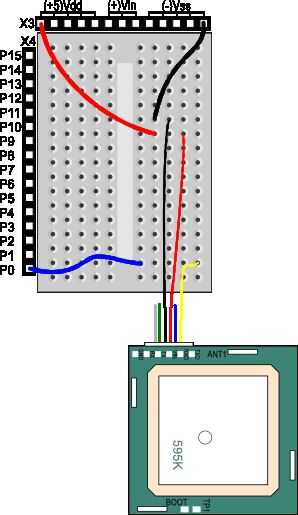
Lamentablemente tuvimos que esperar en que los aviones no tripulados para volar a un designado longitud y latitud o punto de referencia. Aunque somos sólo alrededor de un mes o menos lejos de haber terminado. En mi primer intento de leer la unidad GPS en la paralaje pude guardar todo con éxito en múltiples matrices de bytes. Sin embargo resultaba más difícil conseguir las matrices en una variable float, por lo que llegué a un puesto de control. A pesar de que podía tener acceso a toda la información que necesitaba podía no manipulo correctamente para utilizar funciones matemáticas de flotador. La unidad GPS nos dio la información byte por byte por lo que no hemos podido encontrar una manera de almacenar nuestra matriz distinta en variables individuales del flotador.
PUB readGPS | u, i, v, w, q, j, e, f, g, h, k, d, dec, final, cntr, MN_AT [1], hora [5], datastatus [1], rmcE_W [1], rmcN_S [1], rmclong [10], rmclat [10], spd [5], [2], el modo lat [10], N_S [1], E_W [1], alti [10] longi [10], [2], número [2], indicador [10], calidad tiempo [10], dirección, comenzar, terminar , char
** esto es donde hemos definido todas las variables que necesitaremos para la función de readGPS, plan para almacenar los valores en los arreglos de discos de información necesitamos
repetir
repetir
Yo: = UARTS.rx(GPS)
GPS_IN [v]: = i
Si w == 0
indicador [q]: = GPS_IN [v]
' UARTS.tx (PC, indicator[q])
q ++
** He creado dos bucles repetir el primero es para configurar los contadores a cero cada vez que hay una coma otro contador va hasta hacer un seguimiento de la información que desea acceder en la cadena NMEA. La repetición siguiente va hasta que hay una coma, por lo que sube el contador de w. De lo contrario la siguiente repetir bucle utiliza el contador w para reconocer su lugar a lo largo de la cadena NMEA y coge la información que se almacena en una variable específica. Por ejemplo w == 0 por lo que estamos almacenando el indicador, de esta manera puedo usar una instrucción simple si entonces a darse cuenta de que cadena NMEA la computadora está leyendo (ver más abajo).
Si el indicador [2] == "G" y el indicador [3] == "G"
Si w == 1
tiempo [j]: = GPS_IN [v]
' UARTS.tx (PC, time[j])
j ++
Si w == 2
lat [u]: = GPS_IN [v]
' UARTS.tx (PC, lat[u])
u ++
Si w == 3
N_S [g]: = GPS_IN [v]
' UARTS.tx (PC, N_S[g])
g ++
…….
Si w == 7
número [h]: = GPS_IN [v]
' UARTS.tx (PC, number[h])
h ++
Si w == 9
ALTI [k]: = GPS_IN [v]
' UARTS.tx (PC, alti[k])
k ++
Si el indicador [3] == "S" y el indicador [4] == "A"
Si w == 1
MN_AT [j]: = GPS_IN [v]
' UARTS.tx (PC, MN_AT[j])
j ++
Si w == 2
modo [u]: = GPS_IN [v]
' UARTS.tx (PC, mode[u])
u ++
Si GPS_IN [v] == ","
w ++
Si GPS_IN [v] == '$'
q: = w: = j: = u: = g: = e: = f: = h: = d: = 0
v ++
hasta que == ","
Lamentablemente no fui capaz de obtener la matriz a un valor flotante así que tuve que detener en ello por ahora. Decidimos utilizar una biblioteca de flotador GPS que va a hacer exactamente lo que intentaba hacer excepto encontraron una manera de hacer esto con alguna Asamblea. Por lo que aparece no soy bien bastante versado en el lenguaje de vuelta para obtener la matriz de almacenan en flotadores. Se utilizaron decimales hexagonales y algo de código muy específica que sólo he visto para idioma spin. Independientemente usando la nueva biblioteca soy capaz de acceder a toda la información requerida como variables float para entonces fui capaz de hacer una función de rodamiento donde damos nuestro punto de referencia en longitud y latitud. Usando una fórmula matemática para encontrar rodamiento puedo usar el GPS flotador matemáticas variables de longitud y latitud para calcular nuestro cojinete. El siguiente paso será conseguir el drone para cambiar su curso basado en lo que el cojinete y la Lee de partida. Lamentablemente tuvimos que terminar el proyecto de la competencia debido a e inesperado deja a los países bajos es una semana antes de la competición. Nos dan unas semanas más y debemos tener una completa capacidad de tener la cabeza del robot hacia puntos específicos.
Cojinete de PUB (lon, lat) | dlat, dlon, blon, blat, x, y, b, c, oso
blon: =-121.8576
Blat: = 37.6967
dlon: = fm.fsub (lon, blon)
dlat: = fm.fsub (lat, blat)
a: = fm.fmul(fm.cos(lat), fm.sin(blat))
b: = fm.fmul(fm.fmul(fm.sin(lat), fm.cos(blat)), fm.cos(dlon))
y: = fm.fmul(fm.sin(dlon), fm.cos(blat))
x: = fm.fsub(a,b)
oso: = fm.degrees(fm.atan2(y,x))
** Blon es la longitud final y nuestro blat es nuestra latitud final para nuestro cojinete. Dlon y dlat son nuestra diferencia en longitud y latitud de nuestra partida y nuestros puntos de referencia longitud y latitud. De lo contrario sólo utilizar una fórmula matemática con nuestra biblioteca de matemáticas de flotador y convertir todo a grados para obtener nuestro cojinete.













