Paso 8: Diseño de riego
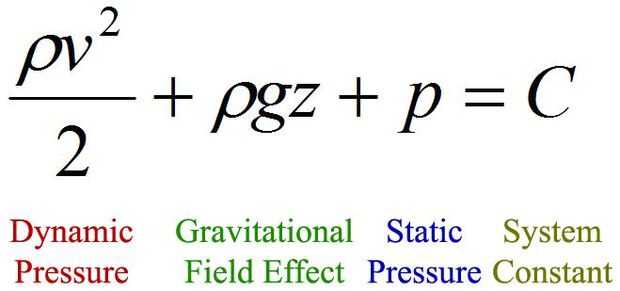
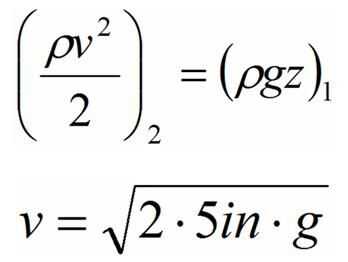
Si usted está contento con saber esto, por favor salte a la siguiente sección, de lo contrario sigue leyendo.
Hay realmente solamente una ecuación que necesita saber para diseñar un sistema de riego por gravedad: ecuación de Bernoulli, como se muestra a continuación.
Esta ecuación es básicamente una reafirmación del principio de conservación de la energía, que sólo se aplica a un continuum incompresible. Agua puede ser asumido como tal para la mayoría de aplicaciones, incluyendo éste. La ecuación indica que para cualquier ubicación, o nodo, dentro de un sistema cerrado, la presión dinámica y el efecto del campo gravitacional y la presión estática será igual a una constante que no cambia de sistema. La presión dinámica es igual a la densidad del agua multiplicada por la velocidad en el nodo, dividido por 2. El efecto del campo gravitatorio es la densidad del agua, multiplicada por la aceleración debido a la gravedad (9,8 m/s2), multiplicada por la altura del nodo, tomado desde un punto de referencia arbitrario pero constante. La presión estática es simplemente la fuerza dividida por el área en el nodo. Por último, la constante de sistema es un desplazamiento constante potencial de todo el sistema, que puede ser cero.
Como un ejemplo simple de cómo usar esta ecuación, sea la elevación de la tierra nuestra referencia de altura vertical y el sistema se construyó de modo que la parte inferior del depósito del agua está a nivel con el suelo. Cuando el cubo llena con 5 pulgadas de agua, ¿cuál será la velocidad instantánea del agua en los emisores? Al examinar un nodo en la parte superior del nivel del agua en el balde, la velocidad que se está moviendo hacia abajo la altura es despreciable, así que hay cero presión dinámica. Para la presión estática, sabemos que la tierra tiene un nivel natural presión de 1 atmósfera, y en la parte superior del agua en el depósito, esto es la única presión en ese nodo. Sin embargo, porque sabemos que el estado final del agua volver a la atmósfera en el planter, podemos elegir ignorar este valor, ya que simplemente será un desplazamiento estático para todo el sistema. Esto deja el efecto de campo de gravitación igual a la constante de sistema en este nodo y define la constante de sistema para todo el sistema y es igual a la densidad del agua, multiplicada por la aceleración debido a gravedad, multiplicada por 5 pulgadas.
Ahora podemos examinar el nodo de uno de los emisores en el lugar que el agua se libera en la maceta. Aquí, nos interesa conocer la velocidad del agua, por lo tanto va resolver para la presión dinámica. Para el efecto del campo gravitacional, definimos esta altura como punto de referencia, por lo tanto, la altura y efecto del campo gravitatorio es cero. La presión estática es una vez más la presión atmosférica de la tierra, que nosotros ya cancelados hacia fuera desde antes; por lo tanto debemos hacer aquí mismo. Y por último, ya calculamos la constante de sistema desde el primer nodo. Esto deja la presión dinámica en el nodo 2 igual que el efecto del campo gravitacional en el nodo 1. La velocidad en el nodo 2 se puede entonces solucionar, como se muestra a continuación.
Para descubrir la tasa de fuga total del sistema, entonces basta con multiplicar esta velocidad por el área transversal del emisor y número de emisores en el sistema. Pero mantenga en mente es sólo la tasa de fuga instantánea a la altura actual de agua en el depósito; como la altura del agua disminuye a medida que pasa el tiempo, la tasa de fuga también disminuirá. Si usted saber exactamente cuánto tiempo su maceta se regó y a qué ritmo, usted necesitará utilizar una escritura un script simple con las dimensiones reales de su sistema. Esto se puede lograr discretizing tiempo (siendo cada paso del orden de segundos) y continuamente calculando la pérdida de velocidad y volumen de fugas en cada paso. Esto se hizo en MATLAB para el sistema que se muestra a continuación para que veáis un ejemplo de los resultados esperados.
Un factor que ha sido ignorado por encima es resistencia en el sistema. Porque las líneas de suministro son cortas y relativamente amplia, podemos calcular la resistencia a ser relativamente baja. Esto es también una ecuación más complicada y algo más difícil de calcular. Debido a la dificultad y mis observaciones experimentales son que es despreciable, la resistencia no será discutida más lejos.













