Paso 4: Matemáticas: conjunto de ecuaciones
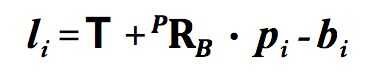
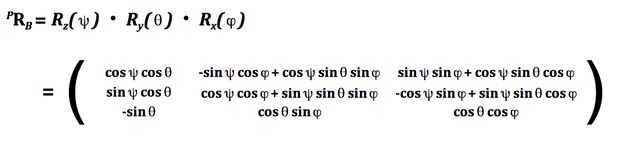
El problema de la cinemática inversa de un Stewart Platform puede dividirse en dos etapas:
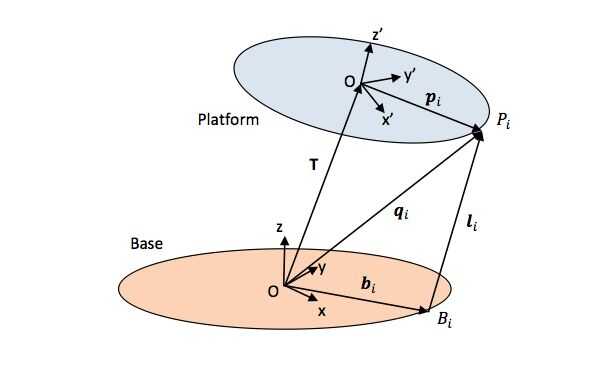
(1) dada una posición y orientación de la plataforma, a qué distancia está cada conjunto en la plataforma de su correspondiente base común,
y
(2) ángulos qué servo, si cualquiera, poner cada plataforma común en las posiciones calculadas en el paso anterior.
El primer problema es fácil de resolver; una vez que tengas los puntos adecuados y sistemas de coordenadas definidos como en la imagen de arriba, se pueden calcular las distancias entre las juntas de base y plataformas juntas con operaciones de matriz simple de rotación y traslación.
Es decir, la longitud de cada pata se calcula utilizando la ecuación de li en la imagen de arriba. T es el vector de traslación entre el sistema de coordenadas de base y sistema de coordenadas de la plataforma (donde desea que la plataforma para mover), bi y pi son las ubicaciones de los empalmes en la base y plataforma de sistemas de coordenadas, respectivamente, y PRB es una matriz de rotación describiendo cómo desea que la plataforma gire. PRB se describe también en detalle en una de las imágenes de arriba.













