Paso 5: Matemáticas: ecuaciones de longitud
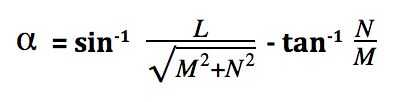
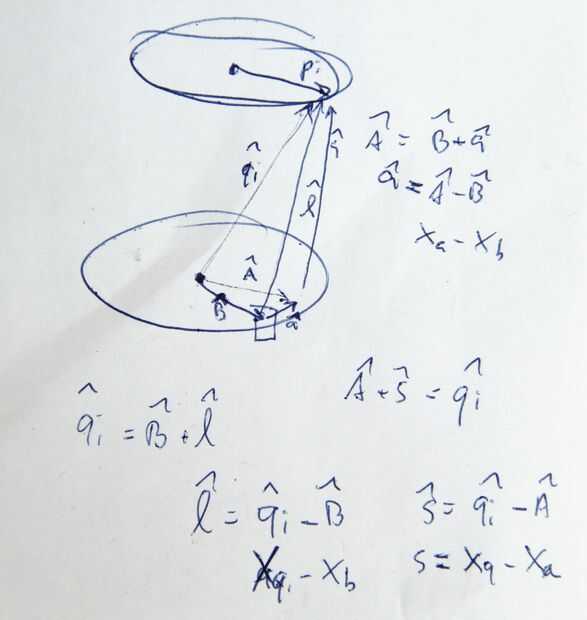
La segunda parte del problema de la cinemática inversa es un poco más complicada. Para cada servo, dada una posición conjunta de la plataforma P, en relación con la posición conjunta de la base B y longitudes para el cuerno del servo fijas una y apoyo la pierna s, cuál es el ángulo de brazo de servo que satisface el l distancia calculado en el paso anterior.
Puesto que l aumenta a medida que varía el ángulo del brazo del servo de-90 ° a + 90 ° (con respecto a plano base), una forma para resolver para este ángulo es hacer una búsqueda binaria sobre los valores de ángulo, y encontrar el que mejor satisface todas las restricciones de distancia. Esto se hace en el código para esta Stewart Platform.
Sin embargo, el documento de Wokingham U3A matemáticas grupo realmente pasos a través de la derivación de una expresión de forma cerrada para este ángulo, usando Algunos bastante dulce geometría, álgebra y trigonometría trucos.
En una de las imágenes de arriba (Lea el documento para la derivación completa y la definición de las variables) se muestra la forma de la ecuación para el ángulo.
Realmente encontramos un pequeño fallo en esta parte del documento U3A: en lugar de utilizar los valores de p para las posiciones conjuntas de plataforma en el sistema de coordenadas de la plataforma, tienes que usar los valores de q, que están en relación con el sistema de coordenadas base.













