Paso 2: Matemáticas tiempo
La principal característica de la cara del reloj de sol es, por supuesto, las líneas que finalmente se utilizará para indicar el tiempo. Es importante que estas líneas en ángulos correctos para asegurar que su reloj sea exacta. La ecuación para determinar el ángulo de cada "línea de tiempo" (Ø) es la siguiente:
Ø = Tan-1(Tan(t)*Sin(L))
Donde: t = el ángulo de 12 en un reloj normal [t(noon) = 0°, t(1:00) = 15°, t(2:00) = 30°, t(11:00) = 15 º, etc..]
L = latitud geográfica donde estás, o donde lo vaya a usar el reloj de sol
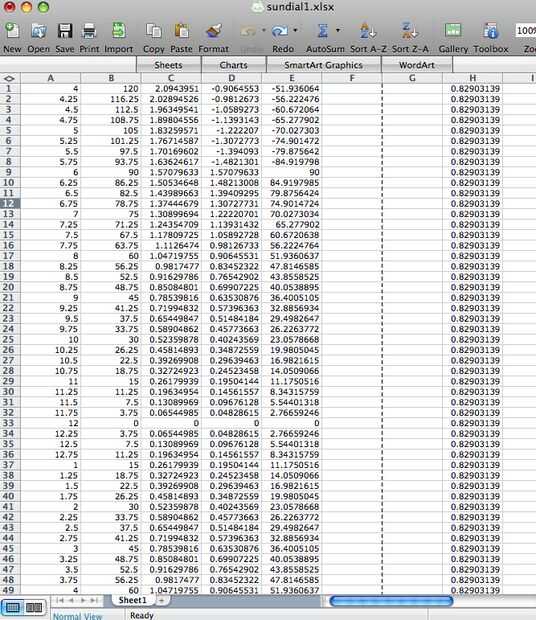
Esto tendrá que hacerse por cada línea que se va a poner en el reloj de sol. Pero no te preocupes, Excel está aquí para salvar el día! Arriba, puede ver una pantalla de captura de mi hoja de cálculo con las ecuaciones usadas en cada columna.
Las líneas pueden ser cada hora, cada media hora o cada 15 minutos (más de lo es probablemente más allá de la precisión del reloj de sol y no vale la pena el tiempo extra y matemáticas). Mina son cada 15 minutos de 4:00 a 20:00.
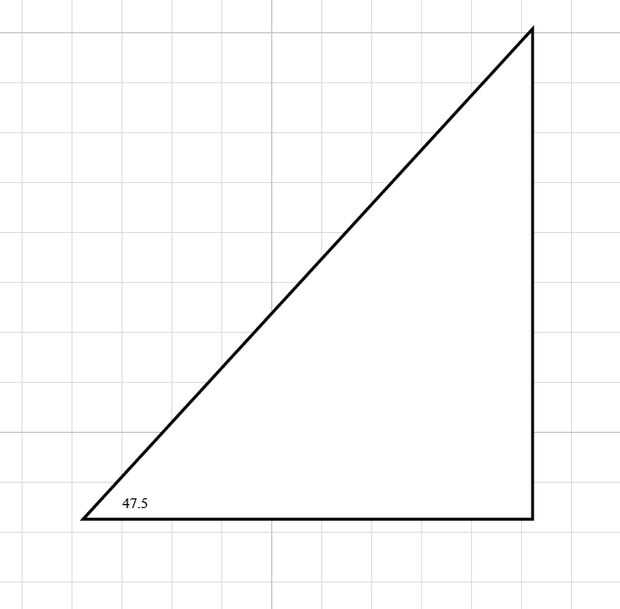
Su latitud también será importante en la fabricación del gnomon (pieza que está parada verticalmente y proyecta sombra en la cara del reloj). El borde superior del gnomon será la parte de la sombra que se alinean con las líneas de tiempo. El ángulo entre este borde y la cara del reloj de sol debe ser igual a su latitud. Aparte de eso, el gnomon puede ser tan simple como un triángulo rectángulo, o un complicado como quieras.
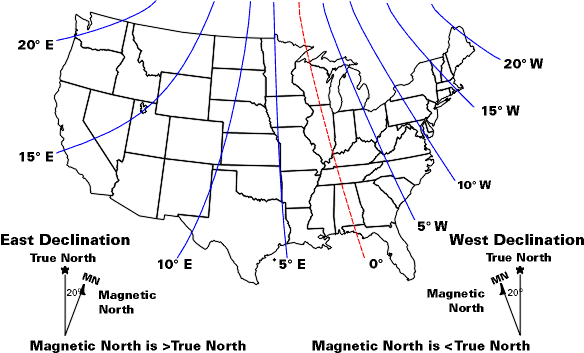
Además de su latitud, un otro valor que se necesita saber es la declinación magnética de su ubicación. Un brújula apunta hacia el "norte magnético", pero para un reloj de sol precisa, necesita saber qué dirección es "true north". Otra vez, esto dependerá de donde están en la tierra y puede ser determinado mediante el mapa de arriba, si se encuentra en la parte continental de nosotros. Lo sentimos, a todos los demás. Sin embargo, estoy seguro que se pueden encontrar mapas similares para otras regiones del mundo.













