Paso 6: Construcciones juego - juego de lógica - detección de colisiones
El balón tiene ahora una manera de moverse de manera predecible, pero ¿cómo la bola la transición entre los diferentes Estados? Lógicamente, ciertos eventos juego dictará las transiciones, pero el siguiente paso es definir cuando los cambios ocurren y exactamente en que estado. ¿Con este diseño de Pong, lo que debería suceder cuando la bola golpea la parte superior y, Análogamente, parte inferior de la pantalla de juego? Romper esto más, golpear la parte superior de la pantalla, la bola se debe mover hacia arriba. Para simular un efecto de rebote, la bola debe pasar a la dirección hacia abajo. Cuando fueron descritos los diferentes Estados de la bola, la bola tiene dos Estados hacia abajo: hacia la izquierda o derecha.
Análisis deben seguir ahora en una base de caso por caso. Por lo tanto, asumir la bola se está moviendo hacia arriba y a la izquierda justo antes de la colisión. ¿Mueve hacia abajo es el siguiente paso lógico, pero debería seguir movimiento izquierda o cambiar a moviendo a la derecha? Si la bola fuera a la transición a un estado de derecho se mueve, la bola revertiría su dirección a lo largo de la diagonal que vino de, nunca hacia el otro lado de la pantalla. La única forma de alcanzar el otro lado de la pantalla de juego es continuar avanzando en una dirección hacia la izquierda. Una situación similar es cuando la bola se está moviendo hacia arriba y derecha: continúe moviendo a la derecha y cambia a una dirección hacia abajo. Simétricamente se manejan los casos hacia abajo.
¿Exactamente Cuándo ocurren estos cambios de transición? Esto implicará la definición de un choque: dos objetos en algún Estado de interseccion se dicen que chocan. En el caso de este juego, que los objetos realmente se cruzan uno con el otro dará lugar a anomalías gráficas; por lo tanto, el estado exacto de intersección será cuando los objetos son tangentes entre sí, o simplemente tocando pero no superpuestos.
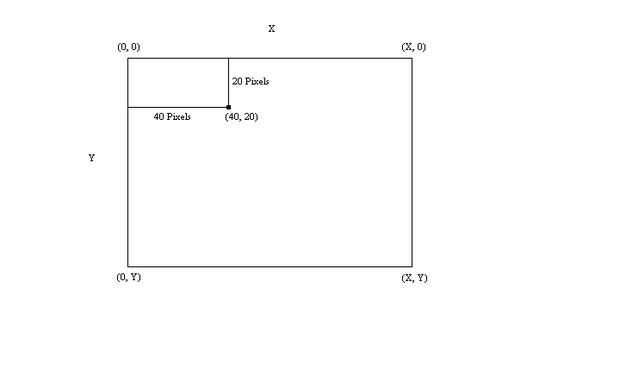
Una discusión sobre el plano de coordenadas está en orden. En muchas idiomas, trazar píxeles funciona de manera similar. Cada unidad en un par ordenado es un pixel con la coordenada x que mide la cantidad de píxeles desde el límite izquierdo de la pantalla y la coordenada y medir la distancia desde la parte superior de la pantalla. La presente resolución sea X x Y, donde X, Y > = 0. X describe la anchura máxima de la pantalla mientras que Y denota la altura de la pantalla. La esquina superior izquierda de la pantalla es (0, 0), mientras que la esquina inferior derecha es (X, Y). Para trazar un punto 40 píxeles de izquierda y 20 píxeles hacia abajo, utilice el par ordenado (40, 20). Por lo tanto, la línea superior de la pantalla puede ser descrita como (x, 0), mientras que la línea de la pantalla puede ser denota (x, Y), donde 0 < = x < = X (ver figura 1).
Resulta que (x, 0) y (x, Y) son los puntos de colisión dentro de la pantalla de juego. Para el primero, la parte superior de la bola será tangente al borde superior de la pantalla de juego y las necesidades de la bola para cambiar al estado correcto antes de realmente en intersección con el borde superior. Ya que todos nuestros objetos juego se describen con las esquinas superiores de la izquierda, cada objeto juego estará representada en datos con algún tipo de par de coordenadas. Entonces el caso de borde inferior funciona de manera similar pero con un pequeño problema. Si la ubicación de la pelota es siempre igual a (x, Y), entonces ya debe estar cruzando el borde inferior de la pantalla de juego. Puesto que la bola es un cuadrado con una longitud constante de s, el punto exacto de la tangente se puede ahora fácilmente calcular. Restando s de Y, la altura de la pantalla produce el punto donde el borde inferior de la bola es tangente al borde inferior de la pantalla de juego. Representando esto en forma de coordenadas par, todos los puntos de posible colisión pueden ser representado por (x, Y - s).
Un conjunto similar de colisiones se presenta el caso cuando la pelota y la paleta no chocan; en esencia, la condición de puntuación. Utilizando la definición del plano de coordenadas (0, y) y (X, y) deben ser los límites izquierdos y derecho de la pantalla de juego, donde 0 < = y < = Y. Dado que las esquinas superior izquierda de los objetos se utilizan para definir su ubicación, la definición del borde izquierdo, (0, y), puede utilizarse para encontrar los puntos de tangencia. Al igual que al encontrar puntos de colisión para los bordes superior e inferior, un caso utilizó la definición de un borde, sino un desplazamiento necesario para encontrar el punto exacto de la tangente. Si la ubicación de la bola era iguales (X, y), la bola ya habría intersecado con el borde derecho. Puesto que la bola tiene un ancho de s, (X - s, y) da todos los puntos de tangencia con el borde derecho de la pantalla de juego.
Todas las colisiones de borde de pantalla ahora sido explícitamente manipularon. Los dos últimos casos son un poco más difíciles, ya que es cuando la bola choca con las paletas en los lados izquierdo y derecho de la pantalla. El cálculo es similar a cuando se trabaja con los bordes de pared-como superior e inferior de la pantalla de juego, pero la pared está limitada ahora, o tiene una longitud muy específica. ¿Dónde la bola realmente puede chocar con una paleta?
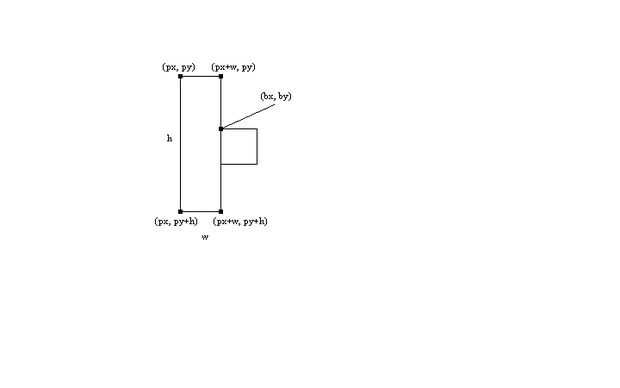
En primer lugar, considerar la paleta izquierda. Dejado h denota la altura de la paleta y w describe el ancho en píxeles. Supongamos que (px, py) es la ubicación de la paleta y (bx, by) describen la ubicación de la bola. (Recuerde, se trata de la parte superior izquierda de las esquinas). Para encontrar el punto de colisión, el borde derecho de la paleta debe ser utilizado. Puesto que la anchura de la pala es una constante (px + w, py) producirá la esquina superior derecha de la paleta. Esto es el límite superior de los puntos de posible colisión con la paleta. Encontrar la esquina inferior derecha rendimiento el límite inferior y así crear todos los posibles puntos donde puede chocar la bola con la pala. Puesto que la altura de la paleta es una constante, se puede encontrar la esquina inferior derecha combinando el borde derecho cálculo y h, rendimiento (px + w, py h). Para realmente verificar la colisión, comparar la situación (bx, by) con (px + w, py h). Así que cuando bx = px + w y py < = by < = py h, una colisión ocurre (ver figura 2).
La pala derecha tiene un problema simétrico con los cálculos. Desde la esquina superior izquierda se utiliza para representar lugares, el borde izquierdo se da prácticamente, así que todos los puntos entre (px, py) y (px, py + h) es los puntos de tangencia posible. Pero ahora el borde derecho de la bola es necesario encontrar la colisión. Puesto que s es la longitud de un lado de la bola, bx+ s da la esquina superior derecha de la bola. El razonamiento anterior puede trabajar ahora, por lo que la colisión ocurre exactamente cuando bx + s = px y py < = by < = py + h.
Una última cosa a la izquierda para discutir: ¿Qué debe suceder cuando la bola choca con las paletas? Si la bola colisiona con la paleta, entonces el estado horizontal tiene que cambiar, de lo contrario la pelota iría a través de la paleta. La siguiente pregunta obvia implica el estado vertical de la bola. Supongamos que la bola se va para arriba; entonces si la bola flip su estado vertical, o bajar, entonces la pelota volvería por su mismo camino diagonal puesto que la bola cambia su estado horizontal. Por lo tanto, el estado vertical debe ser el mismo.
Ahora se aprecia una tendencia interesante entre las relaciones con las colisiones y los Estados de la bola. Si la pelota choca con el borde superior o inferior, mueva el estado vertical. Si la pelota choca con una de las paletas, un borde izquierdo o derecho por decirlo así, del tirón el estado horizontal.