Paso 3: matemáticas

Los valores que sólo recogimos de nuestros cálculos se utilizarán en la Ecuación de lentes delgadas, que es una versión simplificada de la ecuación del fabricante de la lente. Técnicamente, nuestro objetivo no es extremadamente delgada, pero la aproximación hace un trabajo bastante bueno, y evita un montón de matemáticas y de medición. Basado en los datos que recogidos, vamos a calcular la distancia focal de la lente, que es una propiedad intrínseca de la lente del radio de curvatura y nos dice cuánto la lente dobla la luz. Vamos a calcular la distancia focal por dos métodos y utilizar la media de los valores obtenemos (en un intento de minimizar el error).
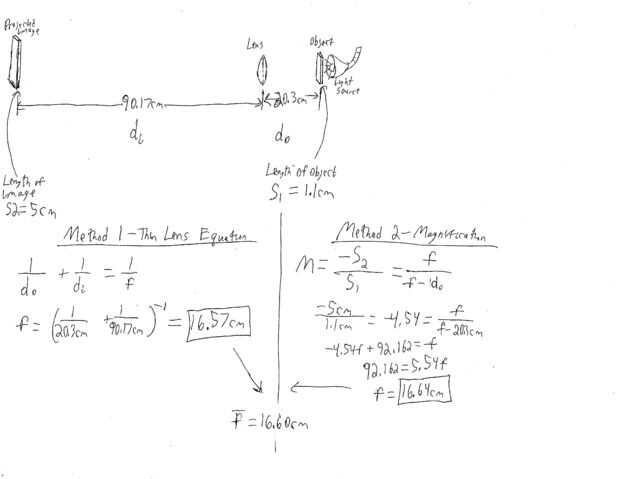
Ver la primera imagen para ambos métodos
Método 1: La ecuación de lentes delgadas
La ecuación de la lente delgada es bastante simple y refiere di, hacer y f. Por mis cálculos, f = 16.57 cm.
Método 2: ampliación
El aumento de la lente es a menudo una característica importante y es simplemente la relación entre el tamaño de imagen para el tamaño del objeto. Aquí, esta relación tiene un signo negativo porque la imagen está al revés. La ampliación se puede también relacionar con f y hacer. Este cálculo conduce a una longitud focal de f = 16.64.
Estos cálculos están en buen acuerdo, con sólo 0,4% de diferencia entre ellos.
Ver la segunda imagen para el siguiente cálculo
Ahora que ya tenemos la distancia focal, podemos determinar el di y para nuestro proyector real. Aquí, me puse di como 177,8 cm (5.83 ft). ¿Por qué utilizar tal un bonito número, pregunte? Bueno, hace los cálculos tan fácil! Justo este número en base cuánto era mi tabla de la pared. Usted puede elegir cualquier número que desee, pero hay algunas consideraciones:
1) cuanto más pequeño el di, el más pequeño, pero más brillante será la imagen
2) el hacer debe ser tal que la lente todavía caben en el cuadro de
Generalmente 150-180cm (5-6 pies) es una buena distancia para di, como la imagen va a ser grande pero aún visible. Una vez que sabes tu hacer y di, ¡ está listo para el siguiente paso!
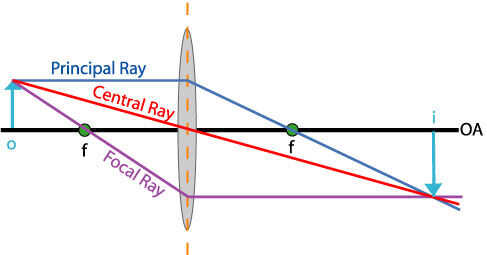
También he incluido un diagrama de rayos para mostrar cómo una lente convexa dobla la luz de un objeto para formar un real imagen. Esto sólo ocurrirá si el objeto está fuera de la distancia focal de la lente. De lo contrario, se produce una imagen virtual (se trata de cómo normalmente se utiliza una lupa).