Paso 11: Funciones trigonométricas combinaciones π aproximado (parte 2)
En el paso anterior encontramos que
Π/4 = arctan(x) + arctan ((1 - x)/(1+x))
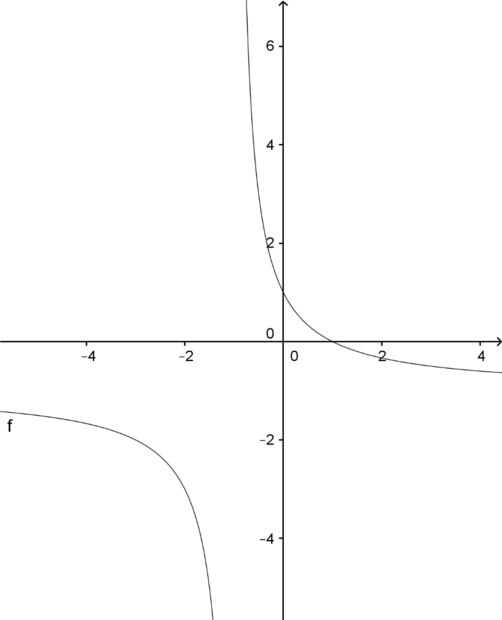
Por lo tanto, si la gráfica de y=(1-x)/(1+x) (ver la primera imagen) entonces el arctan de x coordinar y el arctan de la coordenada y en cualquier punto de la curva se suma a π/4.
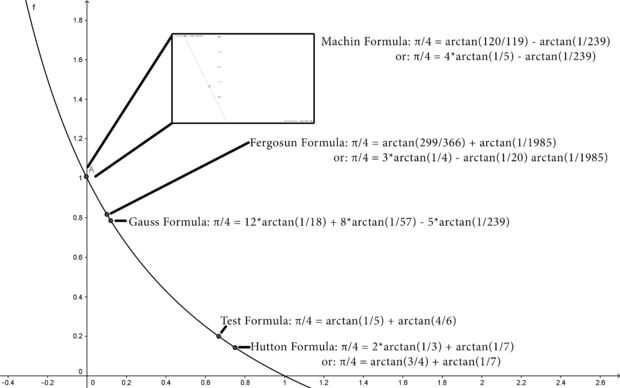
En la segunda imagen que he mostrado cómo otras ecuaciones encontradas por otros matemáticos se encuentran en la misma curva. Cabe señalar que en la mayoría de los casos las fórmulas se divide en tres términos, sin embargo, con el fin de mantener las cosas simples combinan dos de los términos.
De estas ecuaciones vamos a usar fórmula de Gauss que otros han sugerido que proporciona el algoritmo más rápido:
Π/4=12*arctan(1/18) + 8*arctan(1/57) - 5*arctan(1/239)
En el siguiente paso a código esta ecuación y obtener nuestra aproximación de π mejor.