Paso 5: Cómo cambia la longitud del perímetro de un polígono cuando se duplica el número de lados
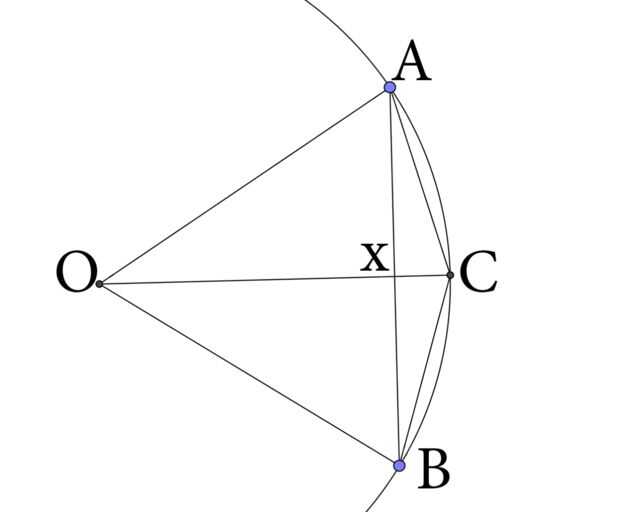
Vamos a considerar un polígono dibujado dentro de un círculo de radio 1, por lo que la longitud de las líneas OA, OB y OC = 1.
Línea OC corta línea AB por la mitad en el punto X.
Sea L la longitud del lado AB de nuestro polígono original y N ser de la longitud de la nueva CA lado.
Por lo tanto la longitud de la línea AX = L/2.
Para calcular N, podemos utilizar Teorema de Pitágoras en el triángulo AXC:
AC² = AX² + XC²
por lo que
N² = (L/2) ² + XC²
Para XC, recuerda OC = 1 y OC = OX + XC, así
XC = 1 - BUEY
que significa
N²= (L/2)² + (1 - OX)² . . . . . . . . . Ecuación 1
Observe que el buey es parte de un triángulo de ángulo recto OXA. Sabemos que OA = 1 y XA = L/2, así que usando Pitágoras en este triángulo encontramos:
OA² = OX² + XA²
que da
1² = OX² + (L/2) ²
así que OX² = 1 - (L/2) ²
Podemos sustituir esto en la ecuación 1:
N² = (L/2) ² + (1 - OX) ² = (L/2) ² + (1 - √ (1 - (L/2) ²)) ²
que simplifica a
N = √(2 - 2 √(1 - (L/2)²))) . . . . . . . . . Ecuación 2
Ahora tenemos una ecuación que relaciona la longitud de los lados L de cualquier polígono dado dentro de un círculo de radio 1 con la longitud de lados N en un polígono con doble número de lados sentada dentro de ese mismo círculo.