Paso 6: Un polígono a partir
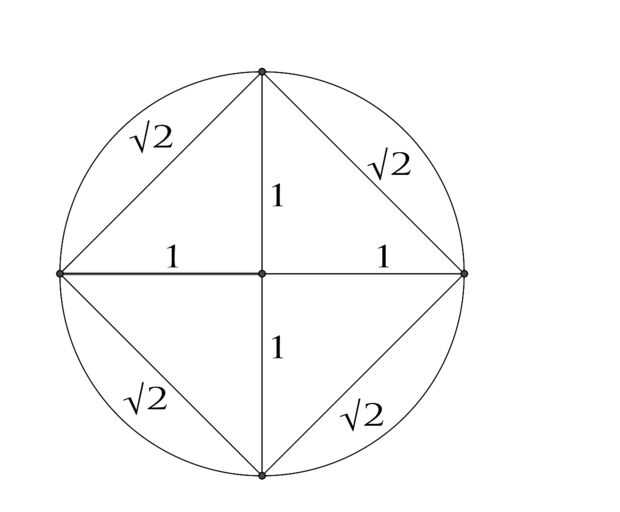
Para poder hacer los cálculos primero necesitamos conocer la longitud de un lado para un determinado polígono. Un cuadrado es un polígono buena para comenzar con como se divide para arriba en la derecha cuatro ángulo triángulos. Los triángulos de ángulo recto todos tienen longitudes laterales uno como están formados de radios del círculo. Así obtenemos:
hyp² = 1² + 1² donde hyp es la hipotenusa del triángulo (y también es la longitud de un lado de la Plaza)
o simplificado:
Longitud de un lado del cuadrado = √2
Por lo tanto, la circunferencia total c del cuadrado = 4 * √2 = 5.66
El círculo tiene radio 1, por lo tanto un diámetro d = 2.
Esto nos da una aproximación muy áspera de π = c = 5.66 / 2 = 2.83
Mejorar la estimación duplicando el número de lados:
Ahora podemos utilizar la ecuación 2 del paso anterior, con L = √2 para calcular la longitud del lado de una forma echada a un lado 8 (un octógono):
N = √ (2-2 √ (1 - (L/2) ²)))
= √(2 - 2 √(1 - (√2/2)²)))
= 0.765
Por lo tanto, la circunferencia total c del octágono = 8 * 0.765 = 6.12
Esto nos da una aproximación de π = c = 6.12 / 2 = 3.06
Observe cómo duplicar el número de lados ha mejorado la estimación de π de 2.83 a 3.06.