Paso 8: Aproximar π usando arctan
El siguiente método implica el uso de la función trigonométrica arctan para crear una serie infinita que converge a π. Primero fue descubierto por Madhava de Sangamagrama, que vivió entre 1340 y 1425.
Este paso va en los detalles matemáticos. Usted puede omitir si quiere ir directamente al algoritmo.
Mediante cálculo se ha demostrado:
arctan(x) = x - (x³/3) + (x⁵/5) - (x⁷/7) + (x⁹/9) - (x¹¹/11)...
¿¿Esto nos ayuda a? Bien la salida del arctan de esta fórmula es en radianes y radianes se definición como el ángulo que se obtiene al dividir una revolución completa en segmentos de 2π.
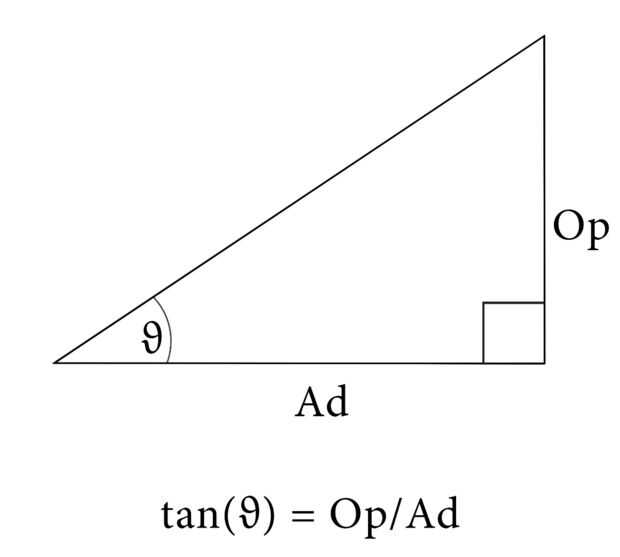
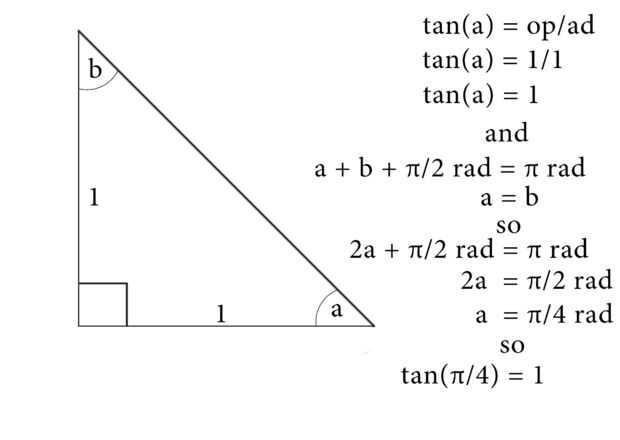
A continuación tenemos que encontrar una manera de relacionarse el arctan fórmula con π. tan (x) es la relación entre el lado opuesto al lado adyacente en un triángulo de ángulo recto con el ángulo x, por lo que si queremos que esta relación sea 1, un todo agradable redondo número, entonces los lados opuestos y adyacentes del triángulo deben ser de igual longitud. Se trata de un triángulo rectángulo isósceles, un ángulo es un ángulo recto, y los otros dos deben ser iguales. Sabemos que todos los ángulos de un triángulos deben agregar hasta radianes π (esta es la regla equivalente a medida todos los ángulos de un triángulo agregan hasta 180 °), y un ángulo π/2 radianes (el ángulo recto). De esto que podemos calcular que los otros dos ángulos deben agregar hasta π/2 radianes, así que cada uno debe ser π/4 radianes. Así que ahí lo tenemos, para la relación entre el lado opuesto y adyacente de un triángulo que uno, el ángulo del triángulo de ángulo recto debe ser π/4 radianes, en otras palabras:
tan(π/4) = 1
Arctan es la función inversa de tan lo sigue:
arctan(1) = π/4
Ahora las cosas comienzan a ser un poco más interesante. Sabemos por la regla:
arctan(x) = x - (x³/3) + (x⁵/5) - (x⁷/7) + (x⁹/9) - (x¹¹/11)...
que:
arctan(1) = 1 - (1³/3) + (1⁵/5) - (1⁷/7) + (1⁹/9) - (1¹¹/11)...
Si sustituimos que en la ecuación arctan(1) = π/4, obtenemos
Π/4 = 1 - (1³/3) + (1⁵/5) - (1⁷/7) + (1⁹/9) - (1¹¹/11)
que simplifica a:
Π = 4 - (4/3) + (4/5) - (4/7) + (4/9) - (4/11)...
Por último tenemos una fórmula perfecta para el cálculo de π! Ahora todo lo que tenemos que hacer es implementarlo en python.