Paso 8: Fractales de L sistema con gráficos de tortuga
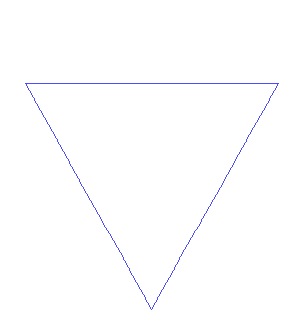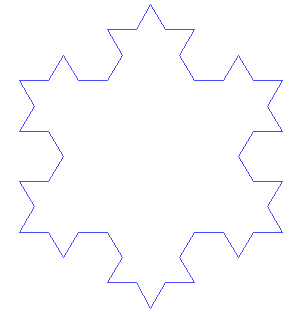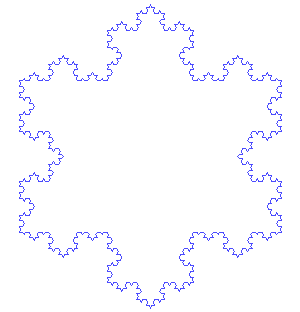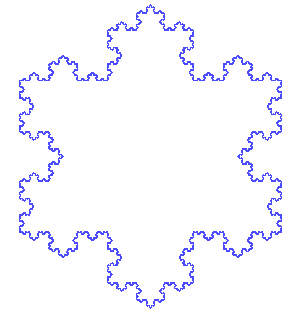
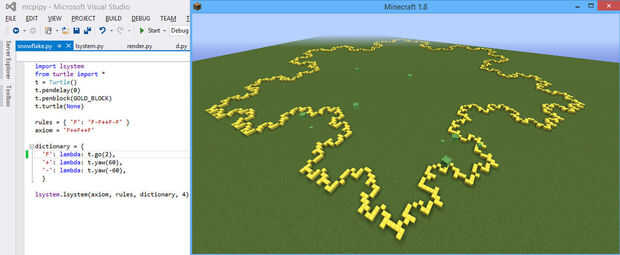
Dibujar un triángulo. Ahora toma cada línea del triángulo y sustituirlo por una línea con una protuberancia triangular en él. Repetir. Como en la imagen animada (dominio público, basado en la

), obtienes un copo de nieve de Koch.
Esto puede ser modelado por un programa de gráficos de tortuga súper sencillos. Imaginar que la F significa "dibujar hacia adelante", y "+" y "-" girar 60 grados, izquierda y derecha, respectivamente. Entonces el triángulo inicial puede establecerse por:
Es decir, ir hacia adelante, girar a la derecha por 120 grados, luego ir hacia adelante, girar a la derecha por 120 grados, seguir adelante.
La línea de la protuberancia triangular puede establecerse por:
Así que aquí está cómo podemos generar un copo de nieve. Tomamos el primer programa de la tortuga F ++ F ++ F para dibujar un triángulo. Cada F en él representa una línea. Tan reemplazar cada F por F F ++ F-F. Si nosotros seguimos adelante, generamos el copo de nieve de Koch.
Este es un ejemplo simple de un L-system. La idea de un sistema de L es que empezamos con una cadena de caracteres (en este caso F ++ F ++ F), y luego un montón de reglas cómo cambiar los caracteres (en este caso, la regla para reemplazar F con F-F ++ F-F) en cada iteración. Esto aplicamos un montón de veces y obtenemos una cadena bastante complicada. Por ejemplo, después de dos repeticiones en el caso de copo de nieve, obtenemos:
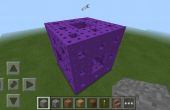
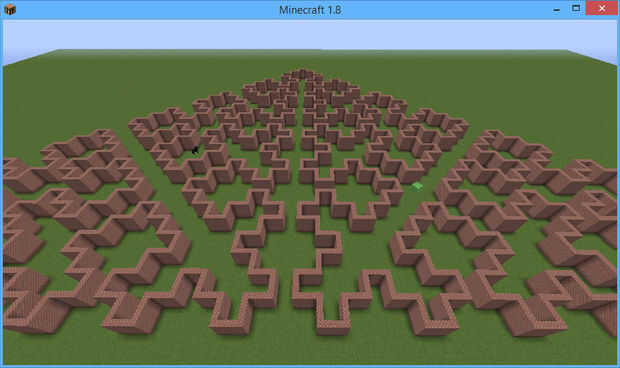
Después de cuatro, obtenemos la imagen de arriba. (Para realmente obtener un fractal, las líneas deben reducir con cada iteración, pero eso no funciona en Minecraft).
Hay mucha información muy buena en este libro PDF gratis.
Escribí un módulo muy simple lsystem.py . Para implementar el copo de nieve, comience con frases repetitivas:
Ahora tenemos que definir las reglas. Definir las reglas por un diccionario de python:
A continuación definimos el axioma, o punto de partida:
Finalmente debemos indicar al sistema lo que cada uno de los símbolos en el medio de cadenas. Para L sistemas, asignaremos significados diferentes a ellos (rotaciones por diferentes ángulos, por ejemplo). Así que tenemos un segundo diccionario de python especificando lo que se hace para cada símbolo. Si no se especifica una acción para un símbolo, el símbolo se omite cuando es el momento de la tortuga dibujar la salida (pero podría ser importante para la generación). Los significados son dados por un diccionario que especifica una función de llamada para cada símbolo. Funciones de una línea se pueden especificar mediante el operador lambda . En este caso, todas las funciones están parcializados:
Finalmente invocamos el sistema L, especificando cuántas iteraciones (en este caso 4):
Hay un truco especial para algunos sistemas de L. Estos sistemas de L son alineado a la red, con todas las rotaciones que 90 grados. El cuadrado curvas (squarecurve.py) y dragon (dragoncurve.py) son ejemplos de Niza. El truco está en llamar, en algún lugar cerca del comienzo de su código:
Esto mueve la tortuga a una ubicación de red entero y alinea su rumbo a una dirección de red. Después de esto, la tortuga permanecerá exactamente red alineada siempre que te mueves sólo por cantidades del número entero (por ejemplo, 7, 7.1 no y no incluso 7. o 7.0 como estos son punto flotante en Python), y gire solamente por la cantidad de enteros que es múltiplos de 90 grados (por ejemplo, -180, o 90, pero no 90.0 o 45). El código de la curva del dragón también da un ejemplo de una función hacia delante que es un poco más complicado, en lugar de sólo una línea, dibuja una pared con una abertura en ella.
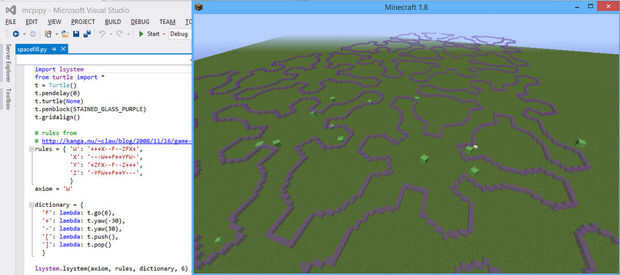
En realidad, llamar a gridalign() a veces puede ser una buena idea aunque no todos sus ángulos son ángulos rectos. Usted conseguirá probablemente algunos problemas de redondeo en una imagen grande, pero todavía puede lucir mejor. Vea el ejemplo de la curva espacial (prestado en vidrio de color morado!).
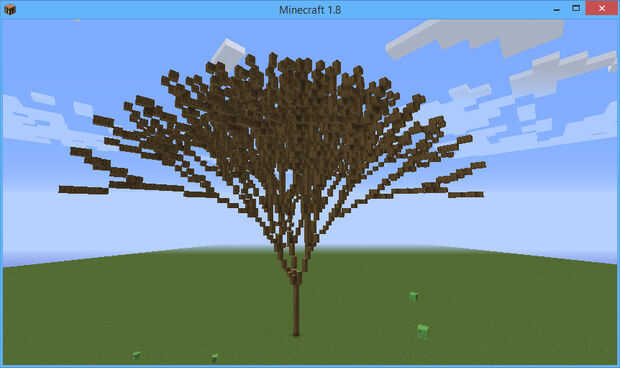
L-systems no tienen que ser bidimensional. Puede incluir símbolos que yaw, pitch y roll rotaciones. Para el diseño de árboles, un truco útil es que comandos de la pila: ' [' para guardar el estado actual del dibujo en una pila y ']' para restaurarla. Esto utilizará los métodos push() y pop() del módulo tortuga. Por ejemplo, aquí está un fragmento de código para dibujar un árbol simple (ltree.py):
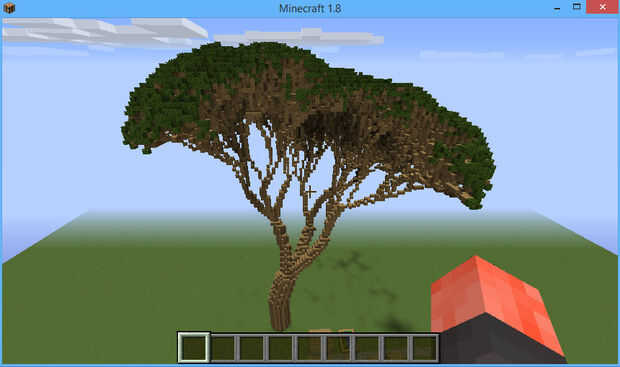
Piensa en la L como una hoja (aunque este código sencillo realmente no dibuja la hoja--que tendría que ser añadido al diccionario). Empezamos con FL, que es un tronco de más de una hoja. Entonces reemplazamos cada hoja por [^ FL] > [^ FL] > [^ FL]. Se trata de un conjunto de tres ramas, cada una inclinada 20 grados del tronco, 120 grados aparte. Los soportes que aseguran después de cada nueva ^ FL es dibujado, estamos nuevamente donde estábamos antes de él. Esto se repite, para que las hojas de las ramas son sustituidas por triples de ramas y así sucesivamente.
Un árbol más realista podría tener el código más complejo para ' ['. Podría hacer los ramas posteriores más cortos y más delgados y cambiar su material a medida que nos acercamos a las hojas (y luego restaurar en ']'). Incluir un árbol como el código de la demo en lsystem.py, basado en reglas (con algunos retoques) del Blogger geek.
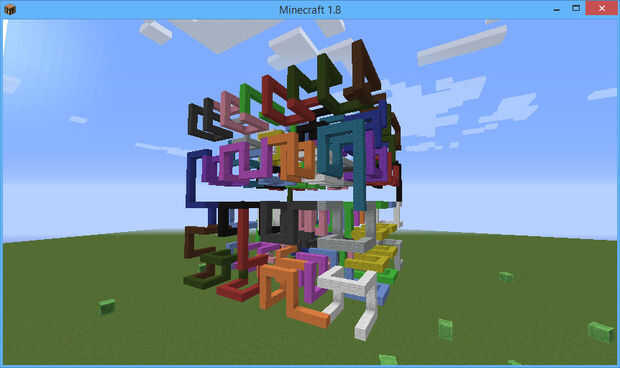
También puede hacer cosas 3D alineado a la red. Por ejemplo, hilbert.py tiene una curva de Hilbert 3D.
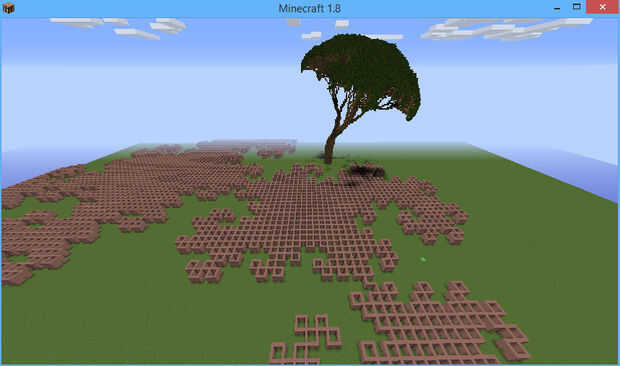
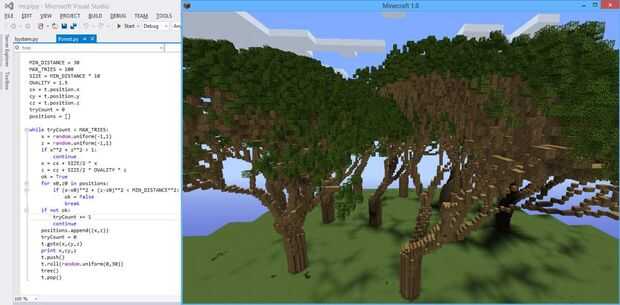
Finalmente, puede introducir algunos aleatorización en las reglas de L sistema. Hasta ahora nuestras reglas eran deterministas: una sola cadena que reemplaza un símbolo, por ejemplo, se dio 'F': ' F-F ++ F-F'. Pero en lugar de una cadena de reemplazo simple, uno puede dar una lista de Python de pares (p, cadena), donde p es una probabilidad (de 0 a 1) y la cadena es la cadena que se utiliza con esa probabilidad. Las probabilidades para un símbolo dado fuente mejor habían no agregar hasta más de 1, pero se pueden sumar a menos de uno, en ese caso, existe la posibilidad de que no habrá ningún recambio. Por ejemplo, aquí es una versión un poco al azar del árbol de .blogger geek:
Esta regla tiene un 55% de posibilidades de sustituir una A con una estructura de tres sucursales y un 25% de probabilidades de reemplazar con una estructura de dos ramas. Esto no es muy al azar, aleatoriedad más haría las cosas aún más realista. Adjunto una captura de pantalla de un bosque bastante dispersos aleatoriamente generado utilizando esta regla (y colocación al azar de los árboles, a una distancia mínima).