Paso 6: Aplicación de quick_sort
Fondo
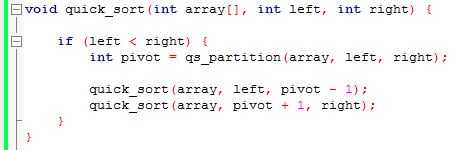
Ahora que hemos escrito la función que hace la mayor parte de la obra, nos podemos llegar a la parte fácil. Nuestra función de quick_sort es muy fácil de entender y se basa en la idea que queremos hacer como poco trabajo como sea posible a nosotros mismos.
Nuestra primera pregunta es: ¿Qué es la matriz más sencilla para ordenar? En mi opinión, es uno con un solo elemento. Si me dan un número, yo puedo ordenar al instante. Vamos a trabajar con esta noción, escriba quick_sort.
Objetivo
Queremos romper el trabajo usando la función qs_partition para nunca tengas que hacer ningún trabajo real.
Pasos
1) primero a ver si podemos evitar trabajo en conjunto. Si nuestro límite izquierdo es menor que el límite derecho, tenemos trabajo que hacer, lamentablemente. Si nuestro límite izquierdo es lo mismo que el límite derecho, la sección que estamos clasificando es sólo un elemento. Si es superior a la derecha, nos encontramos en un estado de error.
2) nuestra próxima estrategia de la evitación del trabajo es decirle a otras personas a hacerlo. Nos a qs_partition y recibe el pivote Índice que se utiliza. Como sabéis desde el último paso, nada en la matriz antes de este índice es menor o igual al valor en el pivote. Después todo es mayor que el pivote.
3) ¿Qué significa eso? Significa que si clasificamos todo antes del pivote y todo después de la pivote, tenemos un arreglo ordenado, porque el pivote ya se encuentra en el lugar correcto. Así que eso haremos. ¿Sabemos que cualquier clasificación algoritmos? Tenemos quick_sort.
Informe
Parece que podemos llegar lejos con no hacer ningún trabajo real. Verás que si llamamos a quick_sort, resulta en dos más llamadas de quick_sort , uno a cada lado de nuestro pivote. Este comportamiento de ramificación continuará hasta que cada llamada se ejecuta en una matriz que es sólo un elemento. Puesto que se ordena un array de un elemento, se ordena toda nuestra matriz.