Paso 1: Proceso de Statististical Control
Para entender el proceso estadístico es necesario entender los siguientes términos:
Nominal es la medida exacta que usted está tratando de lograr. Pero en realidad no es siempre perfecto. Hay variación en todos los procesos, la tolerancia establece los límites de cuánta variación es aceptable. El límite de especificación inferior (LSL) y el límite superior de especificación (USL) son los límites de la tolerancia.
La media es el promedio aritmético de un conjunto de valores, o la distribución. La mediana es el punto donde la mitad de los valores son menos y la mitad son más. El modo es el valor más común. En una situación ideal el Nominal, media, mediana y el modo de todos será el mismo. Usted puede obtener una estimación aproximada de cómo consistente su proceso se está ejecutando, comparándolas.
Capacidad del proceso (CP) es la medida para determinar si el proceso es capaz de sostener la tolerancia permitida. Para encontrar el CP primero encontrará la desviación estándar. La media + (desviación estándar * 3) le da el límite de Control superior (UCL). A continuación encontrar el límite de Control inferior (LCL), medio - (desviación estándar * 3). La capacidad es el cociente de los límites de especificación sobre los límites de control (CP = (USL - LSL) / (UCL - LCL). Si la CP es igual a uno los límites de control caben exactamente dentro de los límites de especificación.
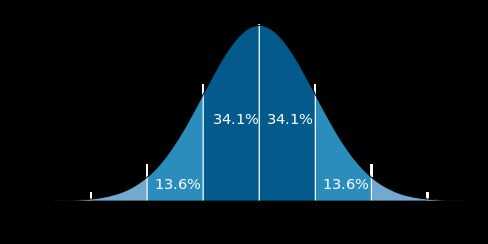
Que desea ser más grande que uno para darle un margen de error. La razón para usar +-tres desviaciones estándar es porque en una distribución normal el 68,2% de los valores caerán dentro de 1 desviación estándar. 95.5% caerá dentro de 2 desviaciones estándar, y 99.7% caerá dentro de tres. Estas cifras son constantes matemáticas conocidos como la Regla empírica. A medida que aumenta la cantidad de variación la desviación estándar también aumentará.
CPK es la medida de lo bien centrado en la media es la Nominal, si son idénticos el CPK será igual a la CP. Más variación entre los dos en cualquier dirección resultará en un CPK inferior.
El estándar más ampliamente utilizado en la industria es un CPK de 1.3.
Las matemáticas aquí se complica, pero es fácil de estimar. Con una distribución normal en el centro de la mitad de la tolerancia con el media centrada en la nominal su CPK serán aproximadamente 1.3. Una distribución uniforme sobre el centro de la mitad de la tolerancia con el media centrada en la nominal le dará un CPK de aproximadamente 1.1. Si el CP y CPK ambos igualan a exactamente un 99,7% de las piezas será dentro de la tolerancia. El a. 3% será mala.













