Paso 2: Corta en lógica difusa
Por principio tengo que escribir algo sobre lógica difusa.
Variables en lógica (booleana) digital pueden ser verdad o falso o "1" y "0" respectivamente. Así que hay sólo dos valores: en la zona (cómoda) o fuera de cierta área (incómodo). Así que solución a nuestro problema con lógica digital nos puede proporcionar solamente con valores de frontera. ¿Pero lo que si podíamos llegar a cualquier valor entre 1 y 0? Sí mis amigos, lógica difusa puede hacer precisamente eso!
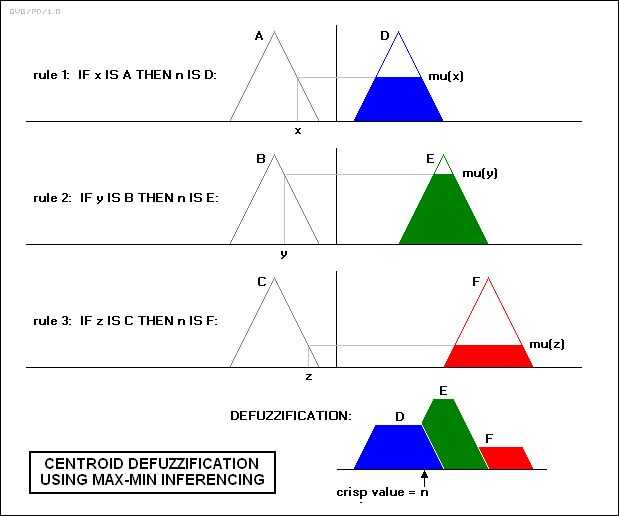
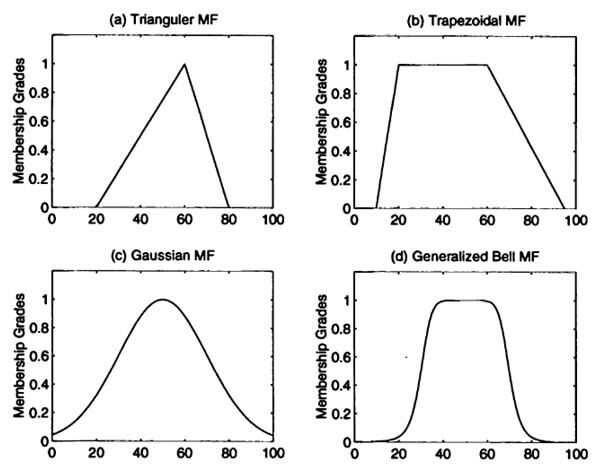
Hay tres etapas en lógica difusa: Fuzzificación, predicción y defuzzificación. Primero algo de Fuzzificación. Fuzzificación es proceso con el cual calculamos afiliación de entrada variable para una determinada población difusa o funciones de pertenencia. Puede haber muchas formas diferentes de funciones de membresía: trapecio, triángulo, Gauss,... En la etapa de predicción estamos utilizando determinado conjunto de reglas (las establecidas por el diseñador) para predecir lo que puede ser la salida o a que miembros función ápice variable afiliados qué nivel de salida. Este número no se puede utilizar como sienta. En la tercera etapa, defuzzificación, podemos combinar todos los niveles de afiliación a un solo valor. Este proceso se denomina también enfoque de valor de salida. Valor de salida solo puede utilizarse luego en la transformación posterior. Más sobre lógica difusa.
Predicciones es lo que hace lógica difusa muy útil cuando las conexiones matemáticas entre las variables no se pueden determinar numéricamente o algebraicamente. Se dispone de varios sistemas difusos para que utilicemos:
- Mamdani sistema (variables de salida lingüística, defuzzificación puede ser complejo)
- Sistema Sugeno (variables de salida son funciones o singleton, constante, más adecuado para la aplicación de microcontroladores)