Paso 2: Las matemáticas
Realmente estaba trabajando en el momento en este proyecto análogo de la veleta, que es básicamente un potenciómetro continuo con un pequeño 'zona muerta' en el norte. Inicialmente, el proyecto fue plagado con esas lecturas ruidos familiar hasta que miré más de cerca a la resistencia.
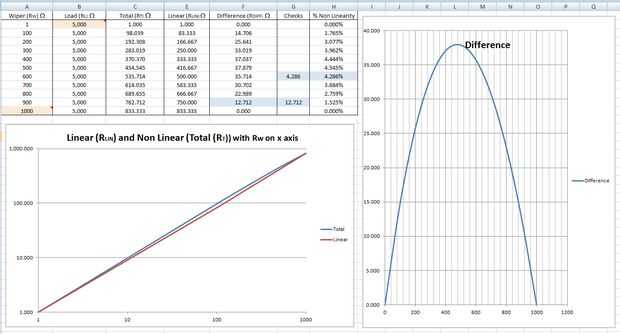
En primer lugar, trazan la curva de resistencia real en Microsoft excel, que es la resistencia total creada por la combinación de la veleta y la carga... y la llamé 'Total (RT)'. Inicialmente, me ha decepcionado no pude realmente ver cualquier curva, así que luego cambié ambos los ejes a log10. ¡ Hey presto! Puedo ver una curva! (La curva azul a la izquierda en el diagrama anterior).
La resistencia total es dada por esta fórmula bien conocida:
RT = (Rw * R L ) / (Rw + RL)
- donde:
- RT es la resistencia total
- RW es la resistencia de limpiaparabrisas
- RL es la resistencia de carga
¿OK, así que ahora tan bien - no demasiado complicado?
A continuación, quería ver cómo se veía mi nueva fantasía curva codo a codo con una curva lineal recta aburrida, como si los resultados no fueron en realidad una curva en todos, sino una línea recta. La fórmula para esto es:
RLIN = (Rw * RTMAX) / RWMAX
- donde:
- RLIN es el hipotética lineal la resistencia (el 'imaginario')
- RW es la resistencia de limpiaparabrisas
- RTMAX es el valor máximo de la resistencia total
- RWMAX es el valor máximo de la resistencia de limpiaparabrisas
¿Esto está muy bien, pero donde vamos a obtener el valor de la resistencia total del? Realmente pensé que esto iba a ser más fácil que esto, pero luego se dio cuenta que ya hemos calculado este valor anterior, es simplemente el valor máximo de RT . Pero sólo por aclaración, aquí está la fórmula:
RTMAX = (RWMAX * R L ) / (RWMAX + RL)
- así que, ahora, si sustituimos a RTMAX obtenemos:
RLIN = (RW * RTMAX) / RWMAX = (RW / RWMAX) * (RWMAX * RL) / (RWMAX + RL) = (RW * RL) / (RWMAX + RL)
Ahora podemos trazar nuestra lineal 'curva' (en rojo) y ver si es perceptiblemente diferente de la curva con curvas... y sí... como nos engañan usando log10, podemos ver la diferencia. Si abrimos el archivo de excel, podemos cambiar el valor de la resistencia de carga para algo estúpido pequeño y obtener algunas curvas bastante locos producidos.
Finalmente, me di cuenta de que entonces podríamos restar la curva no lineal de la curva lineal y obtener un resultado final: la no linealidad real, o la 'diferencia' entre los resultados lineales y no lineales. Esta es la curva bastante azul a la derecha y está dada por:
RDIFF = RT - RLIN = (RW * RL) / (RW + RL) - (RW * RL) / (RWMAX + RL)
Esta ecuación podría reducirse aún más, pero el arduino nano ya va a luchar con algunos de los grandes números producidos (estamos trabajando con ADCs de 16 bits), así que tenemos que ayudar a lo largo de un poco más.
Finalmente, la fórmula se traduce en código de arduino:
Verás que el código es más torpe que la fórmula y he tenido que dividir por 5 para reducir el tamaño de algunos de los números. ¡ Pero funciona!
¿Que he ahora también demostró no que sólo que Matemáticas pueden ser divertido pero también relevantes para el mundo real? ¿Pero lo que este trabajo realmente conseguir?
Si recordamos de antes, la resistencia de carga mínima recomendada era 100K, pero si reducimos estos ohmios podemos hacer las lecturas significativamente más estable cerca de la zona muerta. Probé un montón de diferentes permutaciones y, utilizando la fórmula anterior para negar la no linealidad, que terminó con una muy precisa (+ - 0,1%) Resistencia de 30K y todavía tiene buenas lecturas en due south, que, según nuestro esquema de excel, es donde se producirá la no linealidad de la mayoría.













