Paso 5: Crear las ruedas codificadas



Ahora tengo que escribir las letras del alfabeto en cada rueda en orden aleatorio. Un método para hacer esto es escribir todas las letras hacia fuera en un pedazo de papel. Para cada letra al azar elijo, cruzo fuera de la lista. Empiezo cada rueda con el cubo que sobresale a la derecha. Luego escribo la letra A en un segmento que tiene un rayo. En el habla, escribir un número único. Mi sistema es en realidad sólo 13 ruedas de anchos; mis ruedas son numeradas 1-13. Si tuviera que crear un cypher rodado 26, yo probablemente usaría letras del alfabeto para identificar cada rueda (A-Z).
Crear un sistema de ruedas, cada rueda tiene un único orden aleatorio de letras. A continuación, crear un duplicado exacto de las ruedas para el segundo conjunto.
¿ Si no confías en ti mismo para crear secuencias al azar? Intenta esto:
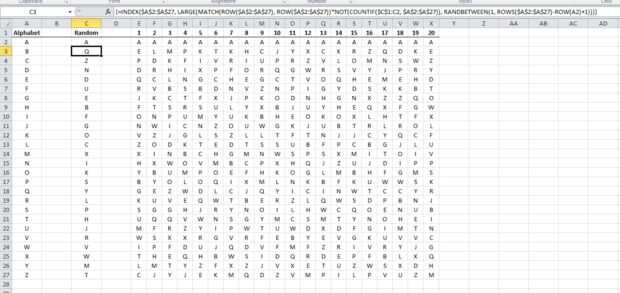
Abra Microsoft Excel. Llenar celdas A2 a A27 con el alfabeto. (Celda A2 = 'A', A3 = A4'B ' = 'C',...) Escriba la letra A en la celda B2. En la celda B3, tipo = índice ($A$ 2: $A$ 27, LARGE(MATCH(ROW($A$2:$A$27), ROW($A$2:$A$27)) * no (contar.Si ($B$ 1: B2, $A$ 2: $A$ 27)), aleatorio (1, ROWS($A$2:$A$27)-ROW(A2)+1))). Pero, en lugar de Presionar ENTER después de escribir en la fórmula, presione MAYÚS + CTRL + ENTER. Esta voluntad temporalmente pone {y} los soportes alrededor de la fórmula. Ahora copia la celda B2 y pegar en celdas B3-B27. Esto creará una única lista de cartas donde cada carta es utilizado una vez. Estos cambiarán cualquier momento hay un cambio en la hoja de cálculo, como escribir el número 1 en la celda C2.
Voy a copiar las letras al azar y utiliza "Pegar especial – valores" para pegar en columnas diferentes para tener un registro de cada rueda.
Para obtener más información sobre esta fórmula, vaya a este enlace:
http://www.Get-digital-help.com/2009/07/03/How-to-...
¿CUÁNTAS RUEDAS DIFERENTES EXISTEN?
Hagamos un pequeño ejercicio para averiguar.
Supongamos que sólo tenemos 2 Letras. Puesto que se trata de una rueda, nosotros siempre podemos que gire la rueda para que la letra "A" es nuestro punto de partida. Como tal, existe sólo 1 combinación posible; AB.
3 letras: abc / acb - 2 combinaciones
4 letras: abcd / avance / acbd / acdb / adbc / adcb - 6 combinaciones.
5 Letras: abcde / abced / abdce / abdec / abecd / abedc / acbde / acbed / acdbe / acdeb / acebd / acedb / adbce / adbec / adcbe / adceb / adebc / adecb / aebcd / aebdc / aecbd / aecdb / aedbc / aedcb - 24 combinaciones
Basado en estas combinaciones, parece que el número de combinaciones podría ser representado por:
n = 2 cartas: (n-1) = (2-1) = 1 combinación
n = 3 letras: (n-1)*(n-2) = (3-1)*(3-2) = 2 * 1 = 2 combinaciones
n = 4 letras: (n-1)*(n-2)*(n-3) = 3 * 2 * 1 = 6 combinaciones
n = 5 Letras: (n-1)*(n-2)*(n-3)*(n-4) = 4 * 3 * 2 * 1 = 24 combinaciones
Este tipo de cálculo se llama un factorial y se representa por un signo de exclamación. es decir 4! = 4 * 3 * 2 * 1
Así que, ya que tenemos 26 letras en el alfabeto. Sacar la letra A, ya que es fijo. Tenemos 25! combinaciones. O:
1.551121e + 25