Paso 1: Determinar si la matriz se puede reducir
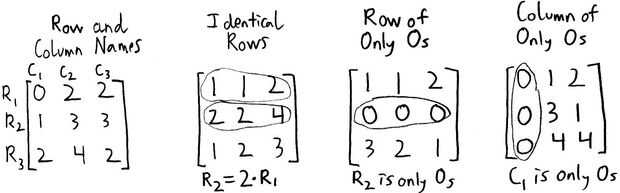
Matrices cuadradas no todos pueden transformarse en reducido fila forma echelon. Estas matrices se refieren como siendo "noninvertible". Una matriz cuadrada será noninvertible si cualquiera de las tres condiciones siguientes son verdadera:
· Una fila es idéntica a, o un múltiplo constante de la otra fila.
· Existe una fila de sólo ceros.
· Existe una columna de sólo ceros.
Un ejemplo de cada uno de estos puede verse en la imagen de arriba. Si la matriz que está utilizando cumple con uno o más de estas condiciones, usted no será capaz de completar los pasos siguientes.
En este Instructable, fila 1 se llamará R1, la fila 2 se llamará R2, y así sucesivamente. R1 es siempre la fila superior, y todas las otras filas se encuentran en orden numérico debajo de R1. Del mismo modo, columna 1, que es la columna de la izquierda, se llamará C1 y todas las otras columnas estarán en orden numérico a la derecha de C1.