Paso 7: Más práctica
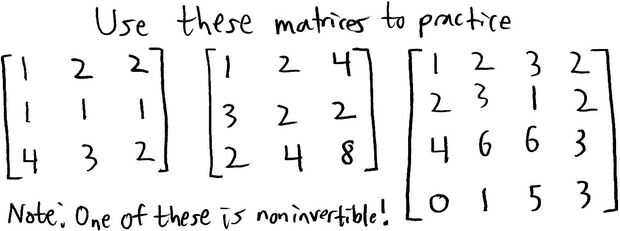
Por encima son algunas matrices más que se pueden transformar en fila forma de escalón reducida. Además, puede crear sus propias matrices con valores aleatorios para utilizar para la práctica. No te olvides de comprobar si es posible para ellos a reducirse con el paso 1.
Este proceso puede parecer trivial en un principio porque el resultado siempre es el mismo. Sin embargo, como se mencionó en la introducción, entender el proceso del uso de las operaciones de fila para reducir una matriz es necesario para otros ejercicios de álgebra lineal como inversión de la matriz y la resolución de sistemas lineales.
Este sitio web muestra paso a paso las soluciones a la reducción de matrices. El orden de los pasos puede diferir de la orden en este Instructable: http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=rref
Este sitio web muestra cómo utilizar este proceso para invertir una matriz: http://www.purplemath.com/modules/mtrxinvr.htm