Paso 3: Prueba de la pantalla

Ahora que nos hemos mudado nuestra exhibición de 4 dígitos a su propio Consejo tenemos que probarlo para asegurarse de que funciona (y a solucionar los problemas inevitables). Esto significa que queremos escribir un controlador sencillo que sólo mostrará un número y compruebe todos los segmentos de cada dígito. Una vez que estamos seguros que todo funciona como debemos entonces puede trabajar en nuestro código de comunicación.
Lo vamos a escribir el código de prueba es para que podamos seguir para más tarde añadiendo simplemente las rutinas de comunicación. Así que nos copia nuestro código de 4 dígitos desde el tutorial pasado y quitar todas las cosas que tenían que ver con el ADC como no estar usando ya. También hemos cambiado los pines de ánodo para que utilicen PC0 a través de PC3 desde hace cableado y codificación más fácil.
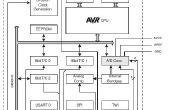
Adjunto el código y un cuadro de la operación de la pantalla externa.
No tengo que ir a través de todo el código línea por línea ya que sobre todo es una simple modificación de las cosas que ya hemos hecho. Sin embargo, hay una cosa que debo señalar.
Finalmente vamos a tener que mostrar números desde el 0000 hasta el 9999 en nuestra pantalla de 4 dígitos. Esto significa que necesitamos 10.000 números de habitación. Sin embargo, un registro de 8 bits sólo va hasta 255. Así que vamos a necesitar más bits dedicado al número queremos mostrar. Vamos a hacer un rápido cálculo para averiguar cuántos bits que vamos a necesitar. Cada dígito es una potencia de 2 y por eso queremos ver qué poder de dos nos da 10.000. Para esto usamos el "logaritmo natural":
2 ^ x = 10000
x ln(2) = 4 ln(10)
x = 4 ln(10)/ln(2) = 13.288
Esto me dice que para 10000 tenemos más de 13 bits. Así que si uso 14 bits entonces tendré más que suficiente. Como un cheque o hacer esto en primer lugar si usted no piensa que matemáticas son divertido, sólo tienes que ir al "la matemáticas es diversión" Web automática convertidor aquí:
http://www.mathsisfun.com/Binary-decimal-hexadecim...
y la figura hacia fuera simplemente convirtiendo. Encontramos que 14 dígitos pueden mostrar números hasta 16383 y 13 dígitos sólo hasta 8191. Así que nuestro cálculo es correcto, que tenemos más de 13 dígitos y menos de 14. Por lo tanto utilizamos 14. De hecho, 9999 en binario es: 0b10011100001111 que es de 14 bits, pero no todos ellos requieren en.
Bueno, para registrar la forma de resolver el dilema de necesitar más de 1 es utilizar 2 de ellos. Esto nos da 16 bits y por lo tanto, es suficiente para mostrar cualquier número que tiramos en la pantalla de 4 dígitos.
Pero cuando enviamos los números a través de nuestra interfaz de comunicaciones que van a estar en binario. ¿Cómo convierte un número binario en dígitos decimales a mostrar? Esto es no casi tan fácil como usted podría pensar a primera vista. Vamos a descubrirlo.
Empezamos con un número entre 0 y 9999 y queremos los 4 dígitos de ese número para que podamos visualizarlos. No hay ninguna función en lenguaje ensamblador que hará eso para nosotros así que tenemos que hacer uno nosotros mismos. El número comienza como un número binario de 2 bytes. Permite llamarlo X por ahora. Nos gustaría averiguar cada dígito a su vez de la más alta a la más baja. El camino nos encontramos con el más alto es que en este esquema de código:
dígito = 0
Inicio:
¿X > 1000?
SÍ:
X = X - 1000
dígitos ++
Goto Inicio:
No:
devolver el dígito
Como se puede ver, esto parece bastante simple. Apenas despegamos de miles uno a la vez y cada vez que aumentamos el valor del "dígito". X no es mayor que 1000 tendremos el número de miles en "dígitos" y nos devuelva. Esto nos dará el primer número de nuestra pantalla. Entonces podemos hacer lo mismo que sobre el restante valor de X excepto con cientos en vez de 1000 esto nos recibirá el número de cientos, y luego hacerlo otra vez con 10 y finalmente cuando no hay decenas a la izquierda, la cantidad restante en X será entre 0 y 9 y así será nuestro último dígito. Así es como podemos obtener los 4 dígitos.
Sin embargo! Es no tan sencillo en lenguaje ensamblador. Una enorme llave es arrojada en este plan debido a que necesitan dos bytes para representar el número binario de 14 dígitos. ¿Cómo restamos 1000? En palabras de 2 bytes, 1000 está representada por 0b0000001111101000 y ves que algo de él está en el primer byte y algo de eso está en el segundo byte. Así que en lugar de X = X-1000 podríamos escribir X como los dos octetos XH y XL así que X = XH:XL y luego hacer la resta como sigue:
XH = XH - high(1000)
XL = XL - low(1000)
¿Eso parece bastante simple derecho? Pues que se pone peor! Supongamos que empezamos con X = 2001 y encontramos nuestro primer dígito (2) restando 1000. Vamos a ver cómo funcionaría:
Prueba X y encontrar que es > 1000 y por lo que nos reste, desde 2001 = 0b0000011111010001 en binario la resta funcionaría de la siguiente manera (poniendo los números en):
XH = high(0b0000011111010001) - high(0b0000001111101000)
XL = low(0b0000011111010001) - low(0b0000001111101000)
que se convierte en
XH = 0b00000111 - 0b00000011 = 7-3 = 4
XL = 0b11010001 - 0b11101000 = 209-232 = - 23
Tenemos un problema! El byte bajo no contiene suficiente para manejar la resta! Se podría pensar que esto no es un problema ya que lenguaje ensamblador pueda manejar los negativos, pero sólo puede manejar hasta un -128 y definitivamente habrá momentos cuando es más negativo que el resultado de la resta de XL. Así que ¿qué hacemos?
Bien, la forma que nos ocupamos de esto es la misma forma que lo hacemos en cualquier resta desde el 5 º grado. Debemos tomar uno de los dígitos de XH. Recuerde que cada dígito binario en XH es realmente igual a 256. Lo hacemos con el comando "sbc" que resta con acarreo.
Luego, una vez que nos hemos librados de los miles que pasemos a los cientos y hacer lo mismo. En ese caso tenemos el mismo problema que tendremos que pedir prestado 1 en el byte alto, hasta que nuestro resultado es inferior a 256 para que seguir con el sbc a subract el byte alto.
Finalmente, cuando llegamos a la 10 y de 1 que ya no tiene que preocuparse de endeudamiento dígitos ya y las cosas son más simples, podemos simplemente restamos el registro bajo.
Así que ahora que ver cómo nos vemos obligados a hacer cosas echa un vistazo al código y ahora podrá averiguar cómo funciona. Observe que hay algunas cosas que teníamos que hacer para mostrar números entre 768 y 999. Puedes pensar ¿por qué puede ser? En cualquier caso, comenzamos dándole simplemente un número para mostrar así que podemos probar nuestra exhibición. Simplemente usaremos 9876. Más adelante nos gustaría el número por venir de otro microcontrolador a través de la interfaz de dos hilos de comunicación.
Ejercicio 1: Averiguar cómo funciona el fragmento de código siguiente.
Aquí está el código explícito que uso para convertir los dos bytes binarios a decimales para los dígitos de la pantalla:
loadCash: ; this computes the digit for each 7-seg of the display<br>cli ; disable interrupts while loading digits<br>push playercashH ; store high byte of playercash<br>push playercashL ; store low byte of playercash<br>ldi tempH,high(1000) ; set tempH:L to 1000<br>ldi tempL,low(1000) <br>rcall computeDigit ; find the 3rd digit<br>mov digit3,digit ; store the new 3rd digit<br>ldi tempH,0 ; set tempH:L to 100<br>ldi tempL,100 <br>rcall computeDigit ; find the 2nd digit<br>mov digit2,digit ; store the new 2nd digit<br>ldi tempH,0 ; set tempH:L to 10<br>ldi tempL,10 <br>rcall computeDigit ; find the 1st digit<br>mov digit1,digit ; store the new 1st digit<br>mov digit0,playercashL ; remaining is 0th digit<br>pop playercashL ; restore low byte of playercash<br>pop playercashH ; restore high byte of playercash<br>sei ; re-enable interrupts<br>ret
computeDigit: ; interrupts are already disabled while here<br> clr digit compareHigh: cpi playercashH,0 ; if both playercashH brne PC+3 cpi playercashL,0 ; and playercashL are zero then done breq returnDigit cp playercashH,tempH ; otherwise continue brlo returnDigit ; if less then move to next power of 10 brne PC+3 ; if high is greater then subtract cp playercashL,tempL ; if highs are equal and lows are less, brlo returnDigit ; then playercash is less so move to next power of 10 clc sub playercashL,tempL ; otherwise subtract power of 10 sbc playercashH,tempH ; otherwise subtract power of 10 inc digit ; and increment the current digit rjmp compareHigh ; and go back up to test again returnDigit: ; digit will now be the one to display in this spot ret
A continuación vamos a introducir algo nuevo--comunicaciones de TWI.