Paso 3: La ecuación del período del péndulo
Con los períodos de cada péndulo seleccionado, el siguiente paso es averiguar las longitudes y los ángulos de los péndulos. Para ello, tomaremos una mirada en algunas ecuaciones.La ecuación para el período de un péndulo está dado por
T=2*PI*sqrt(L/g)*K(θ).
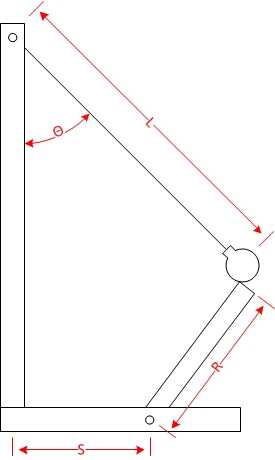
Aquí es una figura que demuestra L y θ. R y S son variables para el mecanismo de liberación, que se solucionará más adelante.
Explicación de términos:
PI = 3.1415926..., etc..
L = la distancia desde la parte superior de la cadena hasta el centro de masa (el centro de la péndola, suponiendo que la cadena es sin masa)
g = aceleración debido a la gravedad (aproximadamente 9.81 m/s ^ 2 o 32.17 ft/s ^ 2)
Θ = el ángulo de lanzamiento de péndulo (el ángulo entre la cuerda cuando el péndulo se encuentra en reposo y cuando se suelta el péndulo).
K(θ) = una función de corrección que toma en cuenta los efectos del ángulo de lanzamiento en el período. Es una serie infinita de energía, pero los sucesivos términos crecen muy pequeños muy rápidamente. Algunos términos son suficientes para obtener una aproximación exacta.
K(θ) = 1 + θ ^ 2/16 + 11 * θ ^ 4 / 3072 + 173 * θ ^ 6 / 737280 +...
Para los ángulos significativamente menos de 1 radián, K(θ) acerca a 1 y se puede descuidar. Para probar si un ángulo es "significativamente menor" que 1 radián, tomar el seno del ángulo en cuestión y, a continuación, compararlo con el ángulo original. Si el ángulo y el seno del ángulo son casi iguales, entonces K(θ) puede probablemente ser descuidado sin grandemente afectar el rendimiento de la onda de péndulo.
Suponiendo que los ángulos de lanzamiento son pequeños y K(θ) pueden ser descuidado, entonces la única variable en la ecuación que debe resolverse para L.
Como algo de un perfeccionista, soy contra descuidar K(θ), incluso para ángulos más pequeños. Decidí ir el más difícil de las dos rutas, sufriendo los más cálculos para (esperemos) una mayor precisión y una mejor rendimiento onda de péndulo.
Por qué algunos péndulo las ondas omitir K(θ) sin embargo, tienen ángulos de lanzamiento grande todavía se ven tan bien?
Este es un ejemplo al azar que he encontrado en YouTube:
En este ejemplo, todos los ángulos son constantes, y así K(θ) también es constante. Como resultado, todos los ejercicios de péndulo son igualmente mal, haciendo todos ellos mira a la derecha en relación con cada uno otro. Para mi onda de péndulo, K(θ) no será constante ya que los ángulos de lanzamiento varían. Debido a esto, no teniendo K(θ) en cuenta definitivamente afectará a las cosas.