Paso 4: Más matemáticas: cálculo de longitud de los péndulos
Hasta ahora, tenemos los períodos requeridos para cada péndulo. También tenemos una ecuación (del paso anterior), que describe el período como una función de dos variables, L y θ y constantes:T=2*PI*sqrt(L/g)*K(θ).
Ya que quiero ver mi onda de péndulo desde la parte superior y necesita las amplitudes de cada onda a aparecer igual desde ese punto de vista, además tengo la restricción:
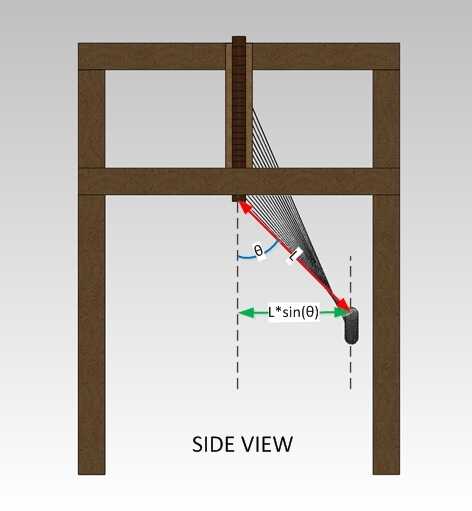
L*sin(θ) = C
donde C es la amplitud constante para todas las ondas.
Aquí es una figura que demuestra este concepto simple:
Mi método para la resolución de la longitud de los péndulos era el siguiente:
1) empezó con péndulo #18 de la serie (el péndulo con la mayor frecuencia y menor longitud), elegir un valor que yo quería para el ángulo de lanzamiento máximo de toda la serie. Elegí pi/4 radianes, o 45 grados. Todo otro ángulo de lanzamiento será menor que este valor.
2) me había conectado este valor para el ángulo de lanzamiento en la ecuación del péndulo, luego había solucionado L durante el periodo necesario.
3) con L y θ ahora resuelto, calculé L*sin(θ) = constante.
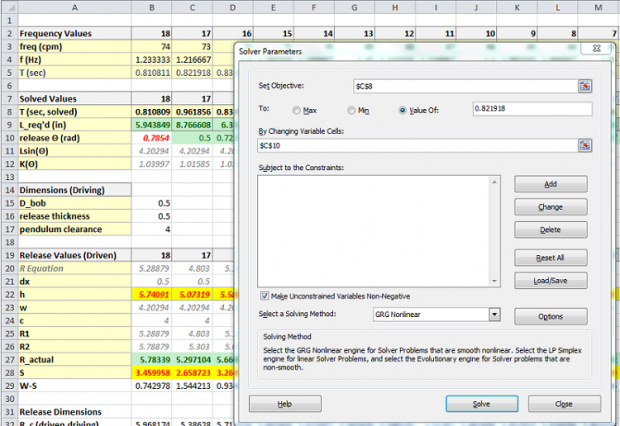
4) para los 17 péndulos restante, utilizado de solver complemento de Excel para establecer la ecuación de período igual al período requerido por el cambio de la liberación del ángulo cuando la longitud = C/sin(θ). Tengo una imagen de este proceso de conexión. Para más información acerca de solver, haga clic aquí.