Paso 5: Lanzamiento mecanismo matemáticas - parte 1
Para el mecanismo de liberación trabajar, cada versión tiene que hacer dos cosas: coge el péndulo y suelte al mismo tiempo cuando los péndulos son la misma distancia (Lsinθ) de la viga de apoyo.Antes de ocuparse de la sincronización para cada versión, averigüemos la geometría primero. Tenemos que encontrar la longitud del brazo de lanzamiento y la distancia horizontal entre el brazo de lanzamiento y el punto de anclaje de la péndola.
El escenario del péndulo se representa en el siguiente diagrama:
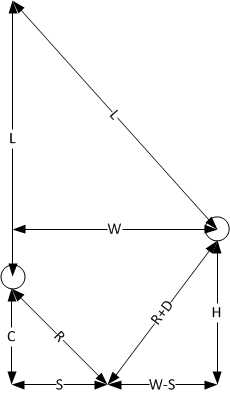
En la figura,
Les la distancia de la viga de soporte del péndulo al centro de la péndola. Este valor se conoce para cada péndulo.
W es la distancia horizontal desde el punto de conexión del péndulo al centro de la péndola en liberación (L*sin(θ), alguien?).
R es la distancia desde el punto de fijación del brazo en la parte inferior de la péndola. Este valor es muy desconocido.
D es la distancia que quiero el brazo para extender más allá de la sacudida cuando recoge el brazo. Para mi onda de péndulo, elegí 0.5".
S es la distancia horizontal desde el punto de conexión del péndulo hasta el punto de fijación del brazo. Este valor también es muy desconocido.
C es la distancia vertical desde el punto de fijación del brazo y la parte inferior de la péndola. Este valor es seleccionado arbitrariamente (elegí 4").
H es la distancia vertical el accesorio de brazo en la parte inferior del péndulo de bob en el comunicado. De inspección, este valor es L-L * cos (θ) + C.
Resolviendo para R y S
Definimos el brazo por dos valores: la longitud del brazo (R + D) y su desplazamiento requerido (S). Permite resolver para estos valores en términos de las variables (conocidas) de conducción.
Para empezar, sabemos que la distancia W es igual a la suma de S y la distancia horizontal entre el S y el péndulo punto de liberación. Usando el teorema de Pitágoras, podemos decir que
W=SQRT(R^2-C^2)+SQRT((R+D)^2-H^2)
Cuadratura de ambos lados de esta ecuación y aislamiento cero da la ecuación cuadrática:
((W^2-R^2+C^2-(R+D)^2+H^2)^2)/4-(R^2-C^2)((R+D)^2-H^2)=0
Se trata de un cálculo doloroso para resolver a mano, así que le sugiere usar un programa como Matlab. Aquí es cómo resolví esta ecuación en Matlab para R:
>> syms R C H W D % definir variables
>> solve([W^2-R^2+C^2-(R+D)^2+H^2]^2/4-(R^2-C^2)*((R+D)^2-H^2),R) % resuelve para R
ANS =
(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 2 * 4 + H ^ 2 * W ^ 2 + W^4)^(1/2) - C ^ 2 * D + D * H ^ 2 + D * W ^ 2 - D ^ 3) / (2 * D ^ 2-2 * W ^ 2)
-(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 4 + 2 * H ^ 2 * W ^ 2 + W^4)^(1/2) + C ^ 2 * D - D * H ^ 2 - D * W ^ 2 + C ^ 3) / (2 * D ^ 2-2 * W ^ 2)
Tenga en cuenta que Matlab nos da dos respuestas porque solucionamos una cuadrática. ¿Qué solución escoger? Para decidir, enchufe en valores razonables, positivos en ambas expresiones y ver qué solución nos da una respuesta razonable y positivo (segunda ecuación).
Por lo tanto,
R =-(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 4 + 2 * H ^ 2 * W ^ 2 + W^4)^(1/2) + C ^ 2 * D - D * H ^ 2 - D * W ^ 2 + C ^ 3) / (2 * D ^ 2-2 * W ^ 2).
Adición de D a este valor (como se muestra en el diagrama) nos da la longitud diagonal del brazo desde el punto de fijación del brazo en la parte inferior del péndulo. Esto es porque el brazo será un rectángulo en lugar de una línea.
R resolver, ahora podemos utilizar Teorema de Pitágoras para resolver para S:
S = SQRT(R^2-C^2).
Bastante simple.
Tenga en cuenta que la distancia diagonal desde el centro de la localización del perno de brazo para el péndulo en el lanzamiento es I+D. Es la longitud real del brazo del pin
R_actual = SQRT((R+D)^2-t^2/4)
donde t es el ancho del brazo.