Paso 6: Lanzamiento mecanismo matemáticas - parte 2
Hasta ahora, tenemos las dimensiones que necesitamos para asegurar que cada brazo agarra el péndulo en la ubicación correcta y lanza en la ubicación correcta. Ahora, tenemos que asegúrese de que todos los brazos de lanzan péndulos todas al mismo tiempo.Después de hacer un pequeño esbozo, surgió un mecanismo simple que funciona. Aparte el brazo, hay dos componentes en este mecanismo. Para meterse con los ingenieros eléctricos, les llamaré el rotor y el estator.

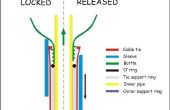
Si la imagen no hace a justicia, es aquí un desglose de cómo funciona la cosa:
Cada brazo (rojo) tiene una ranura cortada en su lado. El rotor (verde) tiene dos espigas, una a cada lado, que se extienden en las ranuras de ambos brazos vecinos. Es clavado en la espalda de dos estatores (azul). Todos los rotores están conectados a una clavija a una distancia constante del perno estator. Así, cuando se mueve un rotor, todos los rotores se mueven a la misma velocidad angular. Con las dimensiones correctas para los rotores y los estatores (ya se han calculado las dimensiones del brazo), los péndulos se pueden lanzar al mismo tiempo.
La configuración para este problema es más fácil de lo que podría parecer.
Resolver para z y Q
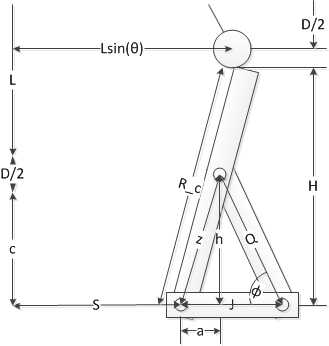
Tenemos que encontrar valores de z y Q, tal que en un determinado ángulo, Ï, la punta del brazo es una distancia horizontal L*sin(θ) desde el punto de accesorio de péndulo.
Ya tenemos S del problema anterior. J es un valor arbitrario (determina el ancho del marco de la onda del péndulo).
R_c es un valor que solucionaremos para más adelante. Es la distancia desde el punto de lanzamiento de péndulo a la línea S. Corre paralela a z.
Para resolver este problema, utilizaremos 3 ecuaciones:
z/h = R_c/H
Q * pecado (Ï) = h
J = Q * cos (Ï) + SQRT(z^2-h^2)
Se resuelve:
z/h = R_c/H = > h = z * H/R_c;
Q * pecado (Ï) = h = > Q = z * H / (R_c * pecado (Ï));
J = Q * cos (Ï) + SQRT(z^2-h^2) = > J = z * H * cos (Ï) / (R_c * pecado (Ï)) + SQRT(z^2-(z*H/R_c)^2)
= > J = z * H * cuna (Ï) / R_c + z * SQRT(R_c^2-H^2)/R_c = > J = (z/R_c) * [H * cuna (Ï) + SQRT(R_c^2-H^2)]
= > z = J/(R_c*(SQRT(R_c^2-H^2) + H * cuna (Ï)))
Y
Q = z * H / (R_c * pecado (Ï))
Problemas para R_c
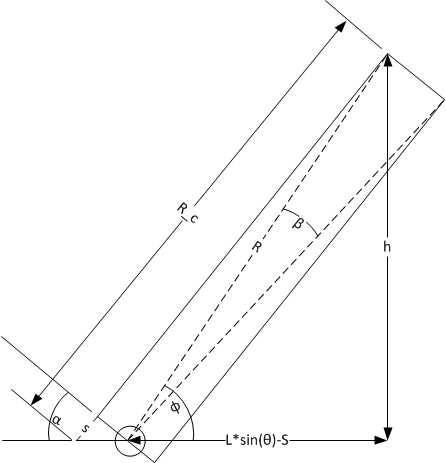
R_c es la suma de s (no grande S de los problemas anteriores) y la longitud del borde del brazo (no mostrado) comenzando en el perno. Como se mencionó en el paso anterior, la longitud real del brazo es diferente que el valor R que se calcularon anteriormente. Además, el ángulo Ï es diferente que el ángulo que ï calculada sólo por encima. Lo siento por cualquier confusión.
La longitud real, por Pitágoras, es:
R_actual = SQRT((R^2-t^2/4)
donde t es el espesor del brazo.
Por lo tanto,
R_c = R_actual + s.
Con el fin de encontrar, tenemos que buscar el valor de α, el ángulo opuesto de s.
En el diagrama, vemos que α = 180 - (Ï + 90 - β/2) = > α = 90 - Ï + β/2
donde Ï = asin(h/R) y β/2 = asin(t/(2*r)).
Así, α = 90 - asin(h/R) + asin(t/(2*r)).
tan(α) = 2 * s/t = > s = t * tan (α) / 2 = > s = t * tan(90-asin(h/R) + asin(t/(2*R)))/2
Por lo tanto,
R_c = t + SQRT(R^2-t^2/4) * tan(90-asin(h/R) + asin(t/(2*R)))/2
Para mi onda de péndulo, elegí liberación el espesor (t) deberá ser 1/2".
Hemos diseñado cada brazo en el mecanismo de liberación para soltar su respectivo péndulo cuando el rotor está en un ángulo constante (Ï). Así, cada rotor puede acoplarse a todos los otros rotores. La implicación de esto es que todos los rotores (cuando) tienen la misma velocidad angular, y los péndulos se liberará cuando el rotor está en ángulo Ï, péndulos de todos serán lanzados al mismo tiempo.