Paso 2: Principio de funcionamiento
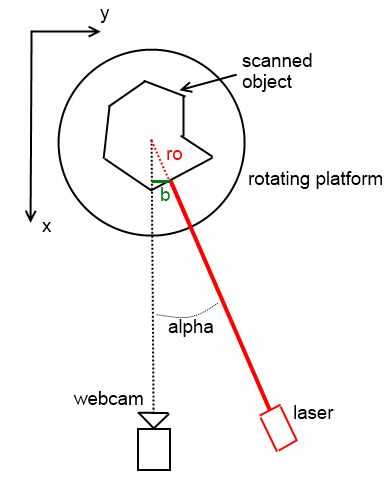
Tenemos que encontrar coordenadas cartesianas (en espacio) de puntos que pertenece al objeto escaneado.
Básicamente, estamos buscando distancia entre el eje de rotación y un punto rojo por láser ("ro" en la fotografía). Para encontrar esto, tenemos que medir cuántos píxeles son entre el eje óptico de la cámara y el punto marcado con láser. En fotografía, esta distancia está marcada como "b". Cuando tengamos esa información, tenemos que convertir en milímetros (cuántos píxeles son de un milímetro). Ángulo entre el láser y el eje de la cámara es constante y es igual a "alfa". Usando trigonometría simple, podemos calcular "ro":
sinus(alpha) = b / ro, que significa que ro = b / sinus(alpha)
Esta operación repite cada capa, en mi caso es 480times. Plataformas giratorias se mueven por un ángulo y repite toda la operación.
Vamos a pasar a la segunda foto.
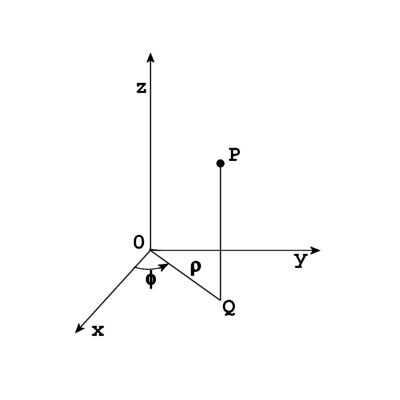
Las operaciones anteriores nos dieron coordenadas en sistema de coordenadas polares. En el sistema polar, cada punto verá algo así:
P = (distancia del eje Z, ángulo entre el punto y X eje, Z) que es P = (ro, fi, z).
Ro es la distancia, medida en la operación anterior. Fi es un ángulo de rotación de la plataforma. Crece una cantidad constante, cada vez que gire la plataforma. Esta cantidad constante en igual 360 grados / número de operación
Es decir, 120 perfiles alrededor del objeto, plataforma se mueve 360deg / 3 = 120 grados. Así que después del primer paso, fi = 3, después de la segunda fi = 6, después de la tercera fi = 9 etc..
Valor de Z es el mismo valor de Z en el sistema cartesiano.
Conversión de polares a cartesianas es muy simple:
x = ro * cosinus (fi)
y = ro * seno (fi)
z = z